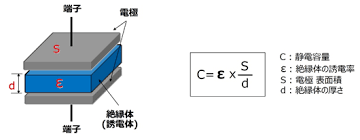
選択問題の問17になります。この問題も、ある公式さえ頭に入っていれば難なく解けたかと思います。
本当に今年の理論は難化しているのでしょうか?本当に去年一昨年に比べれば屁ーこいてプ―なレベルにしか思えないんですけど、、
個人的には理論のボーダー70にして、法規を50に下げて欲しいと願っています。
それではコンデンサの電界問題についてまとめようと思います。
令和2年 電検三種「理論問17」
(a)各コンデンサの極板間の電界の強さを求める問題
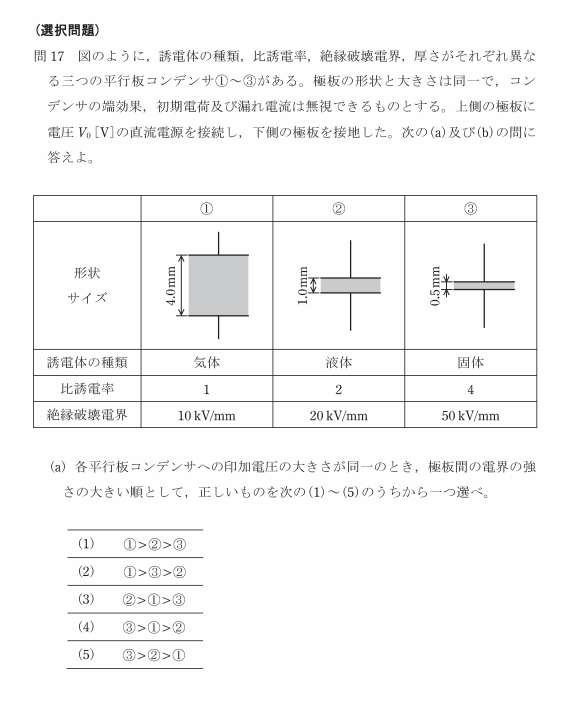
図のように3種類のコンデンサがあり、設問のとおり、極板の形状は同一、端効果無視とあります。
他に、電界に関係しそうな感じで、「極板間の距離」「比誘電率」などの記載があります。
ただし、電界Eを求める下記の公式を知っていれば、「比誘電率」は関係ない事が分かります。
E(電界)=V(電圧)÷d(極板間の距離)
設問aには、印可電圧の大きさは同一とされています。という事を公式にあてはめれば、電界を求めるには残りの「極板間の距離」が分かれば良いことになります。
そして、公式の通り、電界は極板間の距離に反比例することが分かります。
すでに各コンデンサの極板間の距離が分かっているので、各コンデンサの極板間の電界の強さを大きい順に並べるならば、極板間の距離が短い順になります。
したがって答えは、(5)の③②①になります。
(b)絶縁破壊電界時の印可電圧を求める問題

各コンデンサの印可電圧を上げていき、絶縁破壊電界に達した際の印可電圧を大きい順に答えよ、との問題です。
さっきの公式を変換させてみます。
V(印可電圧)=E(電界)×d(極板間距離)
図を見れば、絶縁破壊電界の値が記載されています。つまり、上の公式の電界と極板間距離がすでに求まっているのです。
ですので、絶縁破壊電界と極板間距離を掛けてやれば、それぞれの印可電圧が求まります。
①のコンデンサ
10K(V/mm)電界×0.004(極板間距離)=40V
②のコンデンサ
20K(V/mm)電界×0.001(極板間距離)=20V
③のコンデンサ
50K(V/mm)電界×0.0005(極板間距離)=25V
したがって、答えは(2)の①③②になります。