今回の理論の試験ではけっこう解けなかった方が多い印象です。ブリッジ回路の問題ですね。
まずぱっと見の回路図で嫌気がさした方もいるでしょう。やらしい問題の出し方かもしれません。
しかし、問題文に「ブリッジ回路」とあるので、冷静になればこの回路をブリッジ回路として書き換える事が出来たと思います。
ただ、ブリッジ回路に変換できた後、「平衡していない」事に気づいて、ここでも嫌気がさした方が多いと思います。
二重で罠をかけていますね。
したがってこの問題は、「不平衡ブリッジの計算」が出来る事が必要となります。
王道では「テブナン」を使うそうですが、今回は「デルタ─スター変換」を用いた解き方を解説しようと思います。
スイッチ解放時の1Vうんたらは無視します。
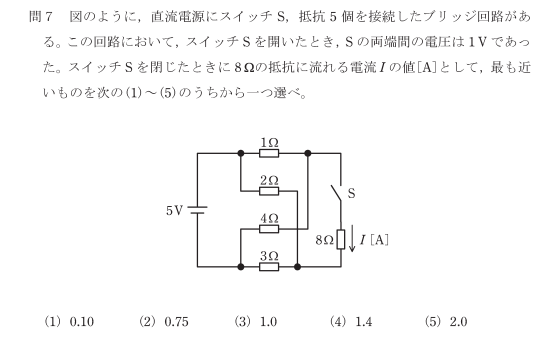
令和2年 電検三種「理論問7」
不平衡ブリッジの電流値計算問題
設問にある通り、この回路をブリッジ回路に分かりやすく書き直せば、下図のようになります。
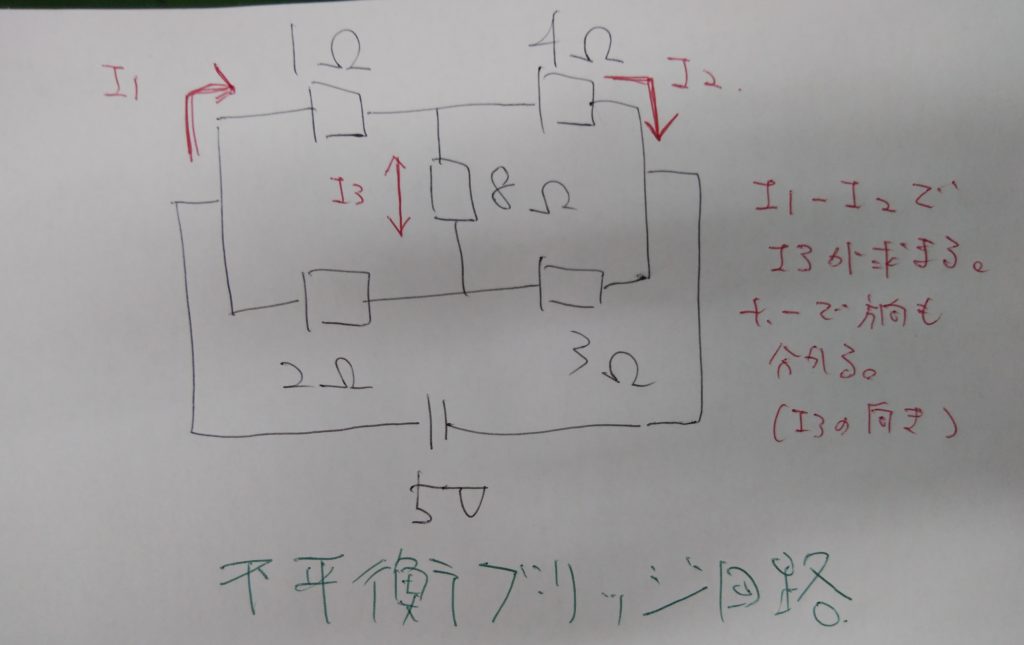
真ん中の8Ω抵抗に流れる電流は分流の法則によって、図の「I1-I2」で求まる事が分かります。
つまり、I3がプラス(I1>I2)の値ならば、電流は上から下へ、マイナス(I1<I2)ならば逆になる事も分かります。
それでは、まずこの不平衡ブリッジ回路を、計算しやすいように分解していきます。
デルタースター変換した回路を2つ作る
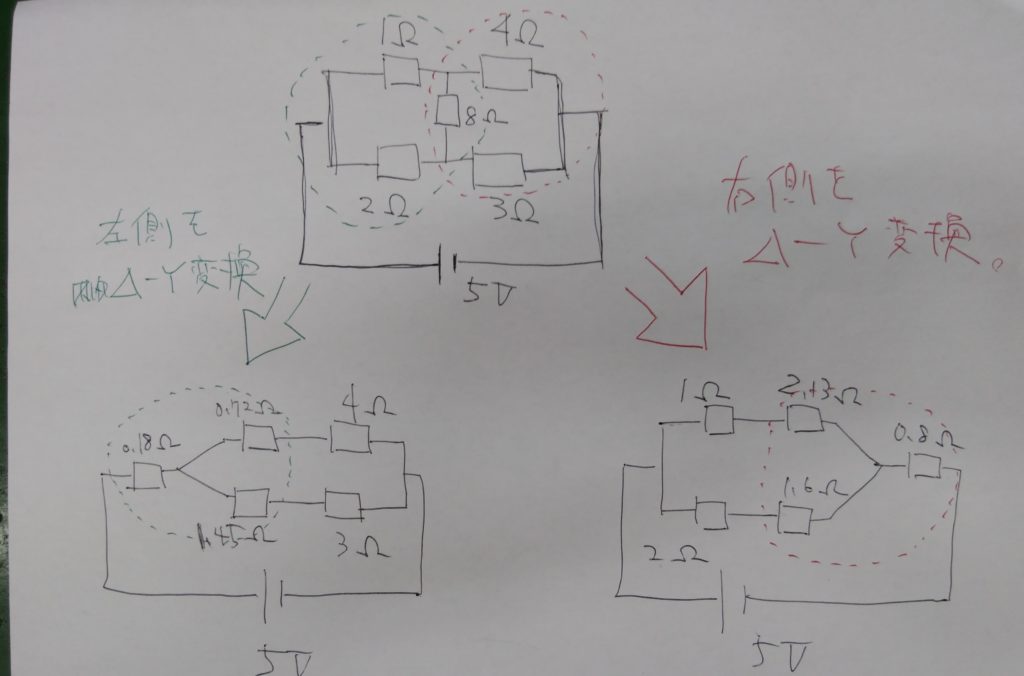
図のように、ブリッジ回路は左右にデルタ回路が成り立っているので、これをスター回路に変換してやります。
※ブリッジ回路のデルタースター変換方法は、過去の記事でまとめています。↓
左と右、両方のパターンを作成します。
左右どちらかの回路の合成抵抗を求める
すると、直列、並列の単純な回路となるので、合成抵抗が求まります。
左の回路の合成抵抗は、Z≒2.47(Ω)
右の回路の合成抵抗は、Z≒2.47(Ω)
上式の通り、もちろん結果は左右同じですので、片方だけ計算すればOKですね。
左右どちらかの回路に流れる電流を求める
したがって、それぞれの回路に流れる電流は、
左の回路全体の電流値=5V÷2.47Ω I≒2.0(A)
右の回路全体の電流値=5V÷2.47Ω I≒2.0(A)
となります。
これも同じですので、片方だけ計算すればOKです。
左右の回路を使ってI1とI2の差を割り出す
左の回路には、0.18Ωで約0.36Vの電圧降下が生じます、したがって、並列回路には4.64Vが印可されている事が分かります。
つまり、冒頭のI1は、左の回路の上側に流れる電流となるので、
I1≒0.983(A)となります。
右の回路には、0.8Ωで約1.6Vの電圧降下が生じます、したがって、並列回路には3.4Vが印可されている事が分かります。
つまり、冒頭のI2は、右の回路の上側に流れる電流となるので、
I2≒1.086(A)となります。
したがって、
I1-I2≒-0.103(A)
答えは(1)の0.1(A)になります。
なお、-の値になっているので、8Ωの電流の向きは上向きに流れている事が分かります。
I1<I2が成り立っている訳ですから。



