需要率・負荷率・不等率
需要率の計算
ふつう需要家は、負荷設備のすべてを一度に稼働させることはありません。
その為、需要家が必要とする電力の最大値(最大需要電力)は、負荷設備容量の合計より小さくなります。
負荷設備容量の合計に対する必要な需要電力の割合を「需要率」といいます。

負荷率の計算
電灯は主に夜間に使われ、クーラーは夏場に使われるというように、負荷は時間帯や季節によって変動します。
この変動の度合いを、次のような「負荷率」によって表します。
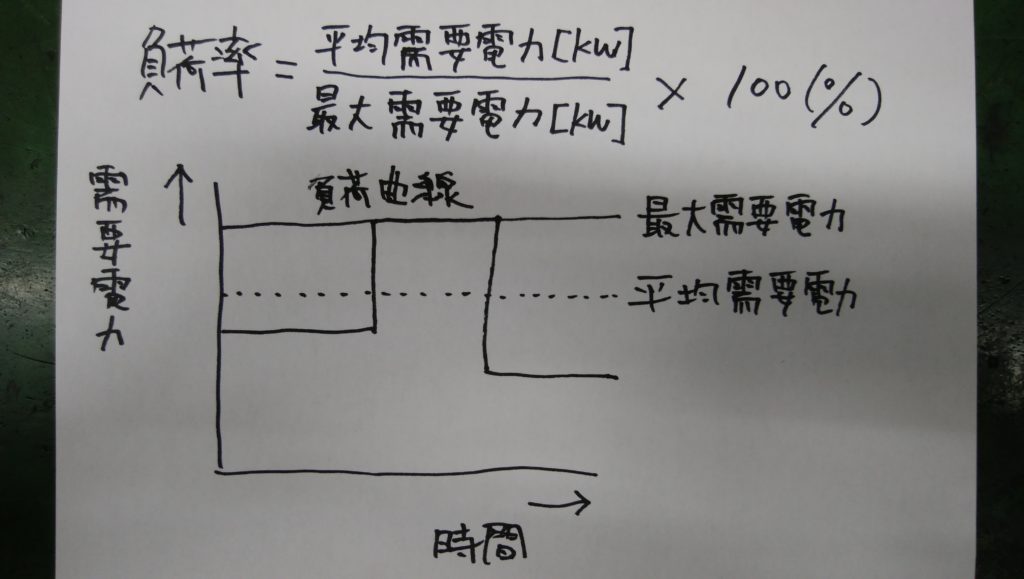
負荷率は、需要電力の平均をとる期間によって、日負荷率、月負荷率、年負荷率などに分かれます。
また、複数の需要家の需要電力を合わせた負荷率を総合負荷率といいます。
不等率の計算
負荷設備を使う時間帯は、需要家によって異なります。
そのため、たとえばある地域全体の最大需要電力は、その地域の個々の需要家の最大需要電力を単純に合計したよりも小さくなります。
この割合を、「不等率」によって表されます。

不等率は必ず1より大きくなります。
力率の改善と電力用コンデンサ
無効電力と有効電力の計算
電力の需要は、電動機や蛍光灯といった誘導性の不可が多い為、一般に遅れの無効電力が生じます。
需要電力をP、無効電力をQ、供給電力(皮相電力)をSとすれば、3つの間には次のような関係が成り立ちます。
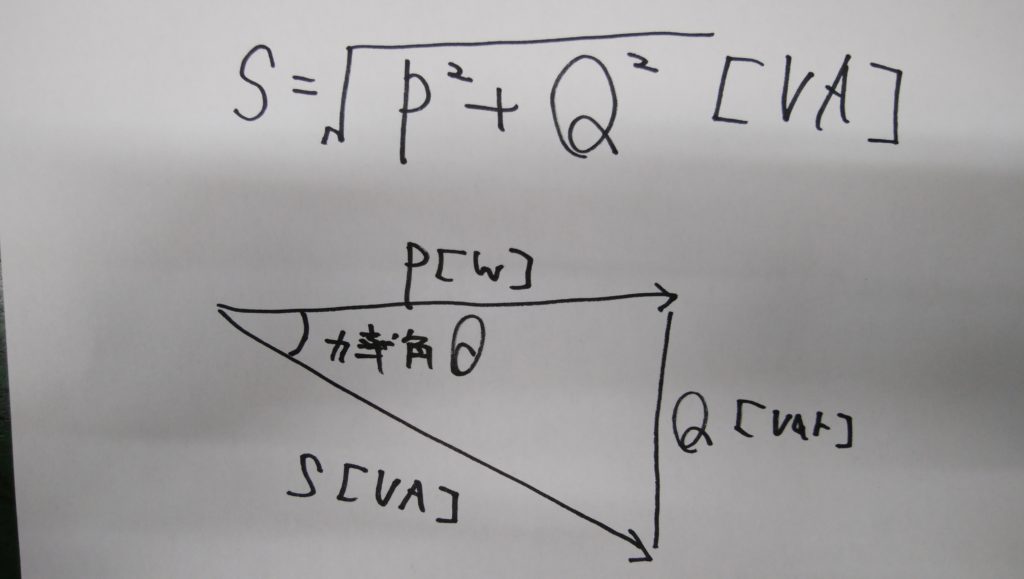
また、有効電力P(W)、無効電力Q(var)は、それぞれ次の式で求められます。
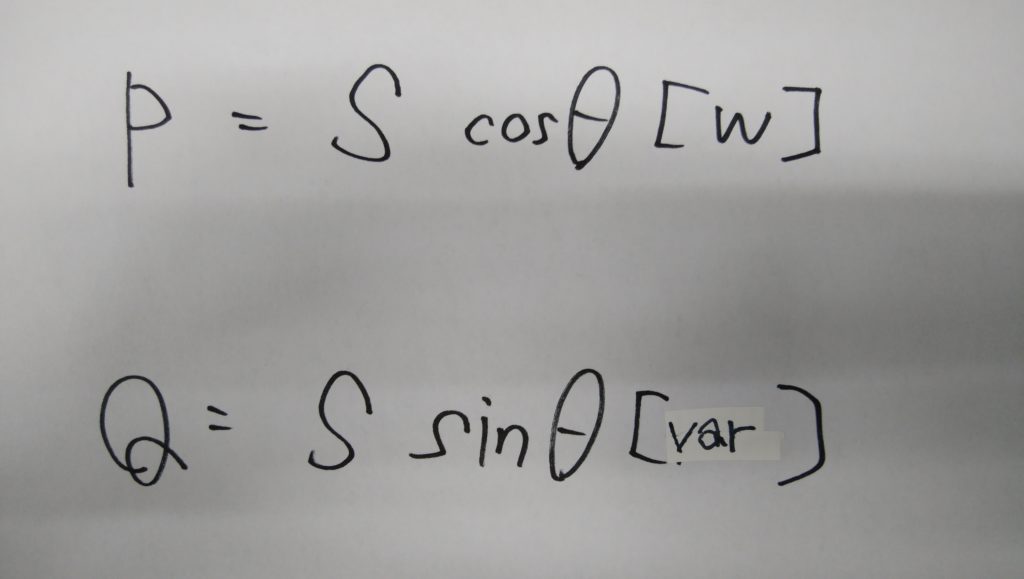
なお、無効電力Qは次の式でも表すことができます。
Q=Ssinθ=S√1-cos^2θ(ver)
力率を改善する
上記のベクトル図より、力率角θが大きくなると無効電力Qが増え、負荷の需要電力Pと供給電力Sの開きが大きくなる事が分かります。
そこで、下図のように無効電力Qと逆の位相をもつ無効電力Q’を流して、力率角を小さくします。
すると、供給電力Sを低く抑える事ができるので、電力供給の効率がよくなります。
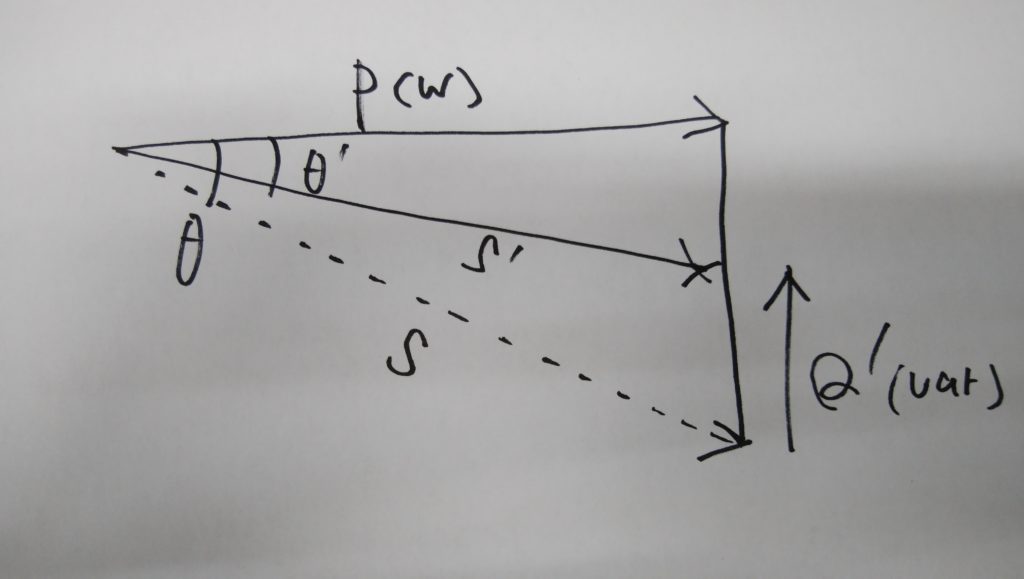
無効電力Qは「遅れ」の位相なので、無効電力Q’は「進み」の位相にします。
したがって、容量Q’(var)の電力用コンデンサを、図のように負荷と並列に接続します。
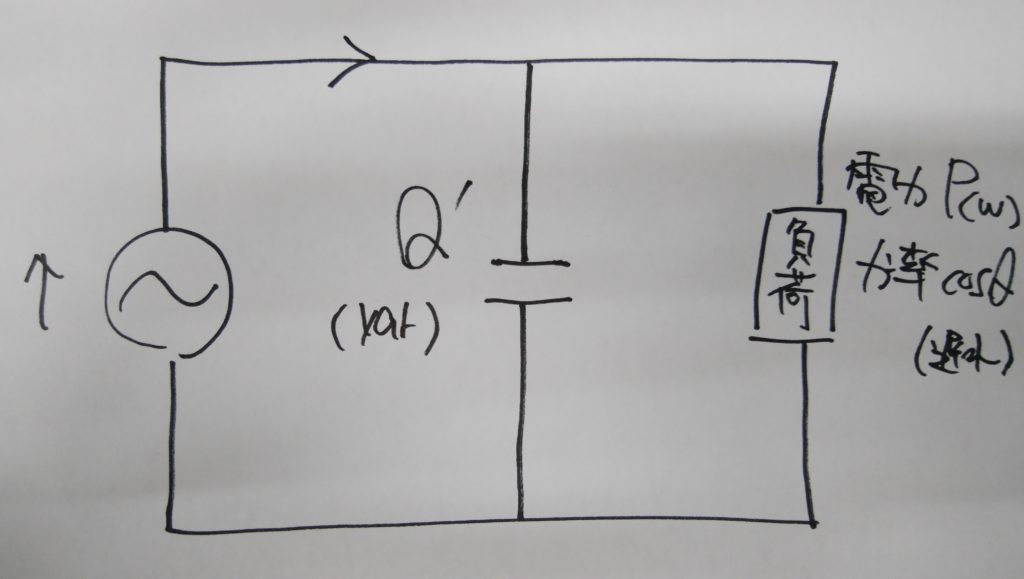
Q=Q’のとき、力率角θはゼロになり、力率cosθは100%になります。
このように、電力用コンデンサによって力率を100%に近づけることを「力率の改善」といいます。


