理論B問題では比較的多く出題されている「3相3線の回路計算」問題。
だいたいa問題が電力値等を求める内容で、b問題が「コンデンサを使用した力率改善」問題になっている印象を受けます。
この問題、aに関しては複素数を使わずに解が求まる事が多いですが、bに関しては「複素数計算」をして答を導くのが一般的です。R,C,Lの並列回路になりますから、通常の計算方法では解くことが難しいんですよね。
ただ、複素数が苦手であるため、このb問題をあきらめている方は多いのではないでしょうか?実際私がそうでした。。
そこで、このb問題の力率改善を「複素数なし」で解く方法もありますので、今回はそれを解説しようかと思います。
それでは、H16年の問16を例として、問題を解いてみます。
H16年の問16 三相三線回路計算問題
問a)線電流Iの求め方
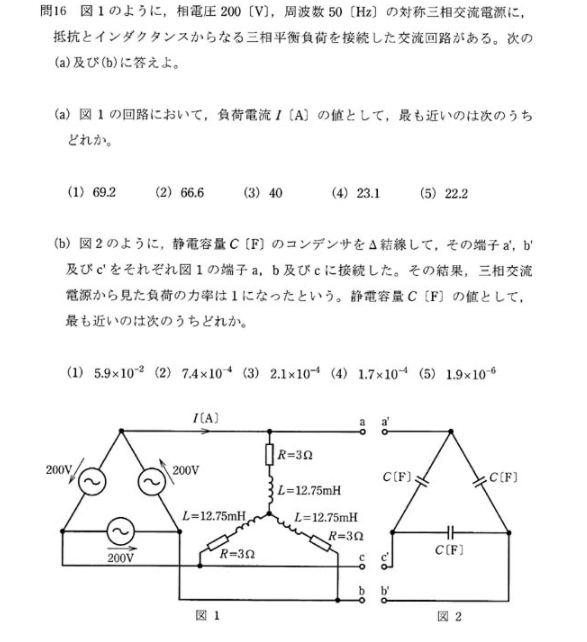
デルタ、スター結線で、負荷に流れる線電流を求める問題です。
図から、スター結線の相電圧は、200/√3になる事が分かります。ですので、あとは負荷の合成インピーダンスZが求まれば、相電流が求まります。
スター結線であるため相電流=線電流になり、それが答えとなります。
それでは合成インピーダンスZの求め方ですが、まず誘導リアクタンスLを求めます。
電源の周波数が50Hzなので、公式「2πfL」に当てはめると、
2×3.14×50×12.75^-3≒4Ω
となります。
1相の合成インピーダンスは直列でつながているので、
Z=√R^2+ωL^2
で表せます。したがって
Z=√9+16=√25=5Ω
となります。
では相電圧を合成インピーダンスで割ってみると、
200/√3/5≒23.1(A)
となり、スター結線なので「相電流=線電流」となり、答は(4)の23.1Aとなります。
ここはイージーだと思います。
問b)コンデンサのデルタ結線を接続し力率改善
図の通り、デルタ結線にコンデンサCを各相に取り付けたものを負荷のスター結線に接続したところ、「力率が1」に改善したという内容です。その時のコンデンサCの値を求める問題です。
初見だと諦めて鉛筆転がすような問題だと思いますが、感覚をつかめばなんとか解ける問題ではあります。
通常、このような問題は、まずCが付いているデルタ結線を、負荷側のスター結線に変更してやります。
力率改善用のデルタ結線コンデンサをスター結線に変更
すると、下記のような「単相2線の並列回路」として見なすことができます。
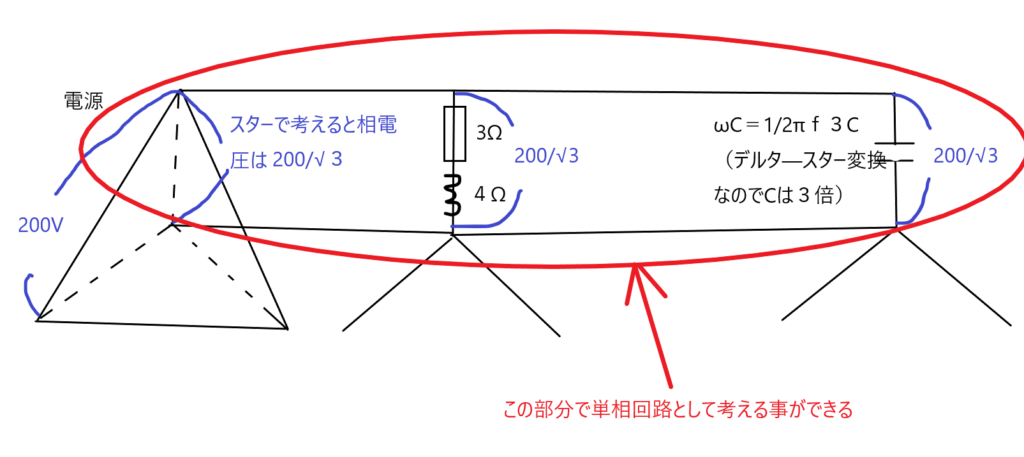
この時注意すべき点が、デルタからスターへ変更時、「コンデンサの静電容量は3倍」になる事です。したがって、容量リアクタンスは「1/2πf3C」となります。
それでは、ここから通常なら複素数を使用していく所ですが、使用せずに解いていこうと思います。
負荷の力率を算出
初めに、負荷の力率cosθを出しておきます。R/Zがcosθになるので、負荷の力率は、
3/5=0.6(遅れ力率)となります。
続いて、無効電力を算出します。
負荷の無効電力の算出
Q^2(無効電力)=V・A^2(皮相電力)-P^2(有効電力)の公式に当てはめて、負荷の無効電力を算出します。
上図のように、回路は単相2線に置き換わっているので、皮相電力、有効電力は下記で表せます。
V・A=200/√3×23.1≒2670(V・A)
P=200/√3×23.1×0.6≒1602(W)
3相3線の場合ですと相間で電力を表す場合、電力は3倍させる必要がありますが、単相2線の為、電力は1倍となります。
皮相電力、有効電力が求まれば、無効電力を求めることができます。
Q^2=2670^2-1602^2≒2136(var)
三角比で表せば下図のようになります。つまり、無効電力である縦成分の2136varを、コンデンサで消してやればいいのです。
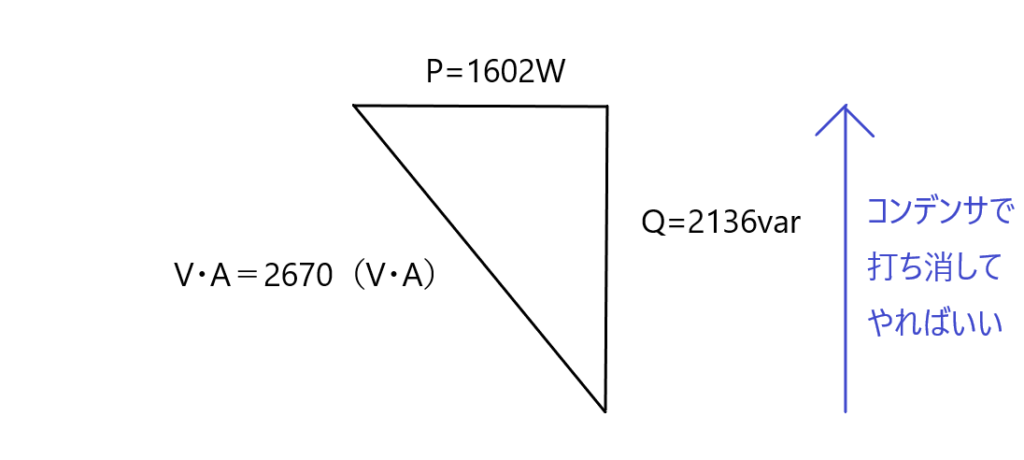
コンデンサの無効電力を算出
並列で入れたコンデンサの回路にはコンデンサしかないので、そこで消費される電力は「無効電力」になります。
つまり、ここの電力を、負荷側の無効電力とイコールにしてやれば、無効電力が互いに打ち消しあって、力率が1になるという事です。コンデンサは進み力率なので、コイルと真逆の無効電力が発生します。
したがって、コンデンサで無効電力2136varを発生させるには、相電圧×コンデンサに流れる電流になるので、まず電流Iを求めます。
2136var=200/√3(相電圧)×I(コンデンサに流れる電流)
I≒18.47(A)⇒コンデンサに流れる電流
容量リアクタンスを算出し、Cの値を求める
相電圧、電流が求まりましたので、コンデンサの容量リアクタンスが分かります。
コンデンサは並列で入ってますが、負荷のインピーダンスとは合成しないので、直列の1/ω3Cで計算します。とすれば、
1/ω3C=200/√3/18.47≒6.26(Ω)
C≒1.7^-4
答は(4)の1.7^-4(F)になります。