理論では時々直流問題にて「ブリッジ回路」の問題が出題されます。
そのほとんどの場合、このブリッジ回路は「平衡状態」であり、真ん中に接続された抵抗や電流計には電流が流れないので、単なる並列回路とみなせるので合成抵抗値を求めるのは簡単です。
しかし、まれに「不平衡」のブリッジ回路の問題も出題されています。
この場合、単純な並列回路とはみなせないので、合成抵抗等の計算に少々戸惑います。
ですが、回路を置き換えてやる事によって、簡単に答えが求まるようになります。
今回は「不平衡」時のブリッジ回路の「合成抵抗」を求める方法を記したいと思います。
不平衡ブリッジの合成抵抗
デルタ→スター変換
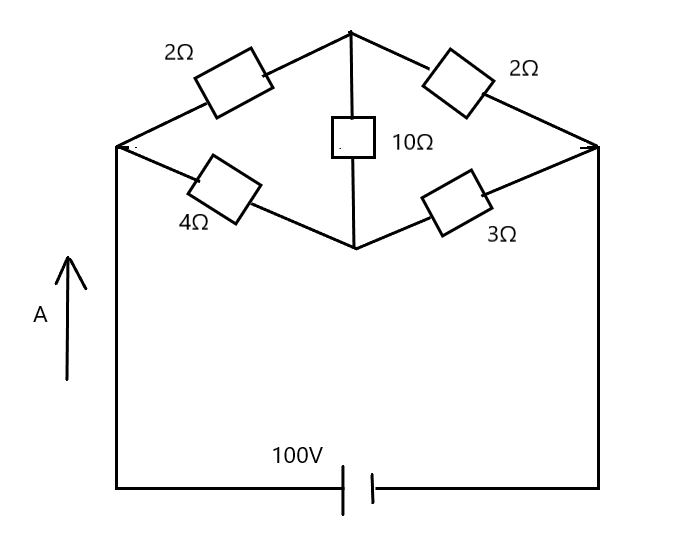
平衡回路では、対角線上の抵抗との積が左右で同じであれば、真ん中の抵抗(今回では10Ω)が省略できますが、図のような不平衡回路であれば、省略ができません。
この問題で合成抵抗を求めるには、一部の回路を変形させる必要があります。
では、左のデルタ回路を、スター型に変えてみます。すると、下記のようになります。
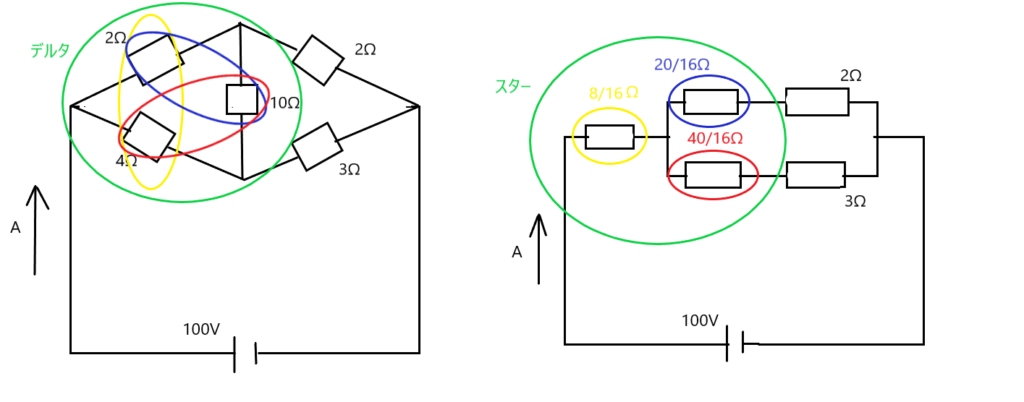
図のように、緑枠部分のデルタ結線をスター型に変更すれば、右図のように直列と並列の回路として考える事ができます。
抵抗値の合成
スター結線に置き換えた抵抗は、デルタ結線の青、赤、黄、の枠で囲んだ抵抗の合成の値となり、右図の位置に配置されます。
合成の値については、デルタ結線の枠の青、赤、黄、の抵抗値の積/デルタ結線の全て(緑枠の3つ)の抵抗値の和、になります。
したがって、スター結線に変更時の抵抗値は、次の通りとなります。
黄色:2×4/2+10+4=8/16(Ω)
青色:2×10/2+10+4=20/16(Ω)
赤色:4×10/2+10+4=40/16(Ω)
つまり、スター結線時に配置する抵抗の位置によって、分子の値が変わります。分子の値は、色分けしたデルタ結線部の抵抗の積になります。分母は、デルタ結線時の抵抗の和となります。
スター結線に変更できれば、後は簡単に合成抵抗を導き出せます。
Z≒2.54Ω
したがって、電流値は
100/2.54≒39.37A
となります。


