電検三種の理論、コンデンサや電界に関する問題で、比較的よく出題される中に「電荷に働く力」「電荷により発生する電位」があります。
この2つは公式が似ており、かつ答えが出るまでの道のりも非常に似ているので、勘違いして間違いやすいのです。
公式としては、まず下記のようなものがあります。
※電荷をQ(C)、真空の誘電率をε0(F/m)、距離をr(m)とします。
Q/4πε0r^2 ・・・ 電界の強さを求める公式
Q1Q2/4πε0r^2 ・・・ 2つの電荷間に働く力を求める公式
Q/4πε0r ・・・ 電荷よりr(m)離れた場所の電位を求める公式
注目すべき点が、電荷による電位を求める場合は「r(距離)は1乗」になる所です。ここが間違いやすい所ではあります。
電荷間に働く力を合成する問題、電位を合成する問題でこれらの公式をよく使いますが、「合成」する際にまた気を付けるべきポイントがあります。
端的に言えば、電荷間に働く力の合成は「ベクトル」で、電位の合成は「スカラ量」になります。
それでは過去問を例題とし、解説していきたいと思います。
H17年度 問1
各点電荷に働く力を求める問題
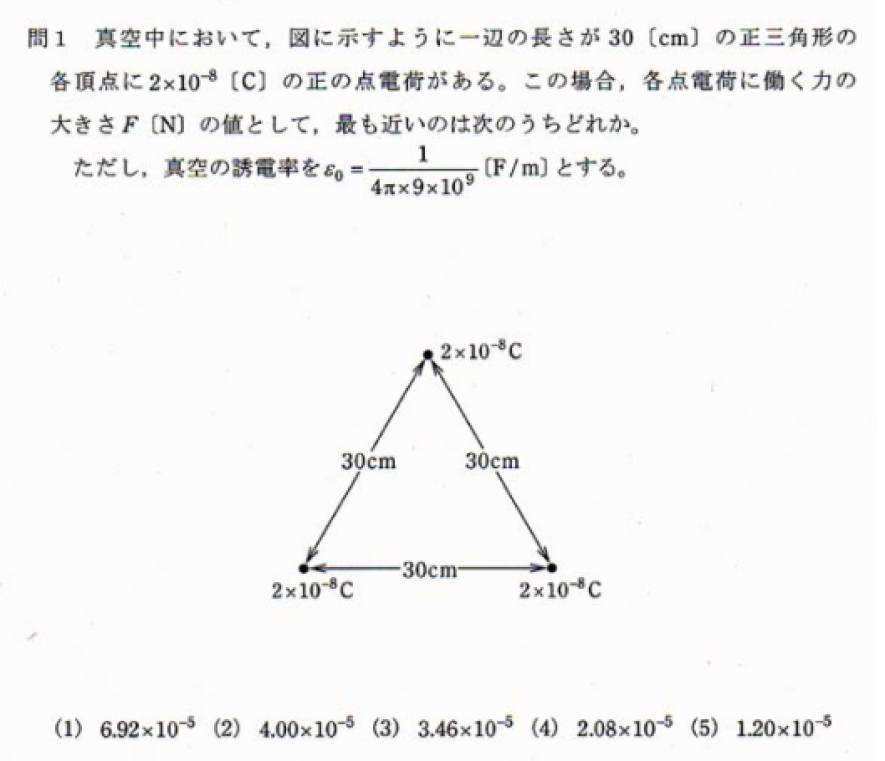
同じ値の点電荷が3つあり、それぞれ距離は30cm、つまり正三角形になります。
1つの点電荷に働く力は、他の2点の点電荷との間に働く力の合成となります。
つまり、頂点の点電荷から時計回りに順にQA、QB、QC、とすれば、電荷QAに働く力は、
QAQB/4πε0r^2(N)
と
QAQC/4πε0r^2(N)
の合成した値となります。
点電荷は全て「正」なので、互いに反発する力が生じます。
この式を解いた値は、下図のような方向に力が発生すると考えられます。
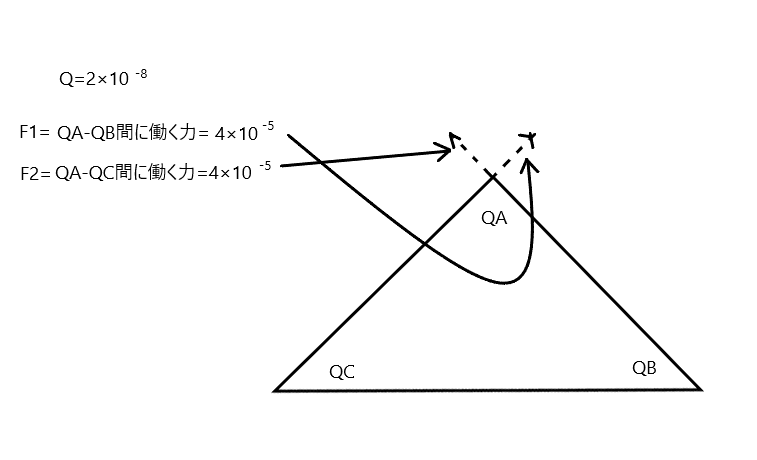
これだと力が分散しているので、ベクトルを合成させてみます。
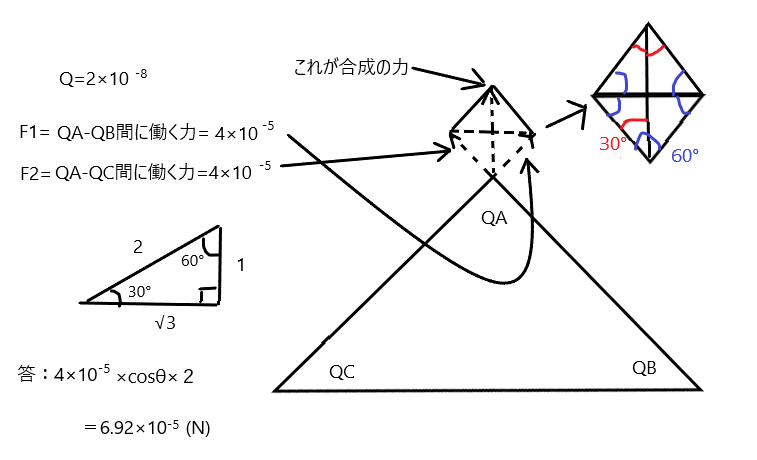
図のように、正三角形を半分にすると30°、60°、90°の1:2:√3の三角形ができます。
つまり、左に書いた三角形の√3の部分の値を2つ足せば、答が求まります。√3の部分の長さは 4×10^-5×cosθになるので、
4×10^-5×cosθ×2=6.92.×10^-5(N)が合成の力の値となります。
答(1)
各電荷は同じ値で、距離も同じなので、上記の答えが全ての電荷に加わる力になります。
このように、電荷間に働く合成の力を求める際には、「ベクトル」で計算する事が多いです。
H17年度 問2
電荷により発生する電位を求める問題
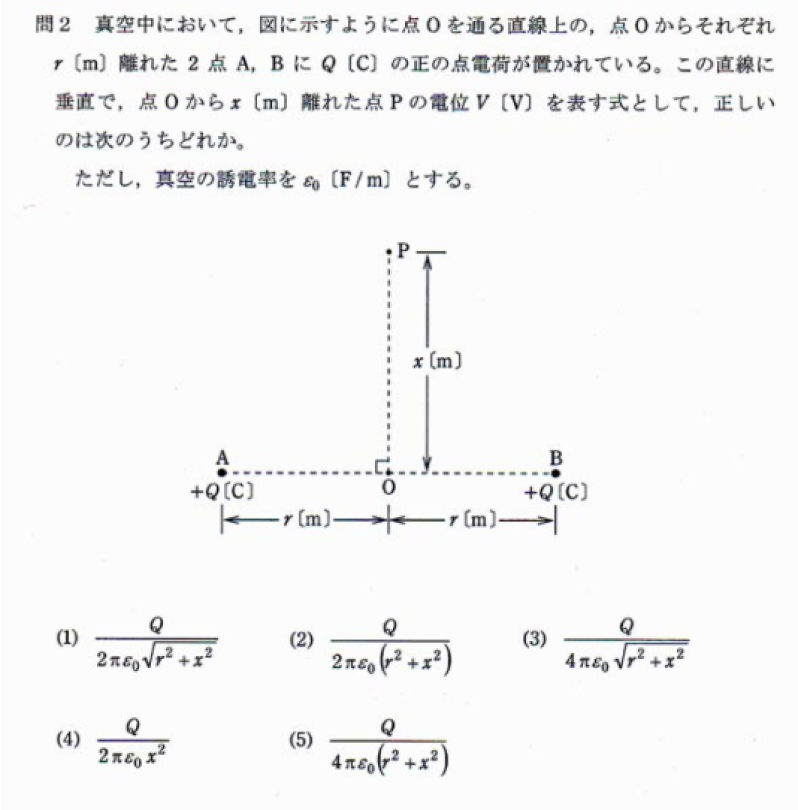
点Pの「電位」を求める問題になります。
問題のとおり、点Pの電位を求めようとすれば、
Q/4πε0r の式を使います。電荷は2つあるので、まずAの電荷から点Pまでの電位を求めます。
ピタゴラスの定理により、AからPの距離は √r^2+x^2 になります。これを式に当てはめれば、
Q/4πε0√r^2+x^2(V)となります。
Bの電荷から点Pまでの電位も、Aの電荷と同じで距離も同じなので、上記と同じ電位となります。
あとはこの値を合成するだけですが、ここが注意点になります。
「ベクトルは使わない」です。P点を突き抜けてそこからベクトルで長さを算出する必要が無いんですね。
電位の合成の場合は、単に「足す」だけになります。ですので冒頭に書いた「スカラ量」的扱いでOKなんです。
したがって答えは、
2Q/4πε0√r^2+x^2(V)2Qが割れるので、
Q/2πε0√r^2+x^2(V)
答(1)となります。


