少しひねった文章ですが、落ち着いて考えると非常に簡単な問題だったと思います。
共振についての基礎が頭に入っていれば、引っ掛けの文章を解読してすんなり答えが導き出せると思います。
令和2年 「電検三種理論問9」
RLC交流回路の電圧と電流のベクトル問題
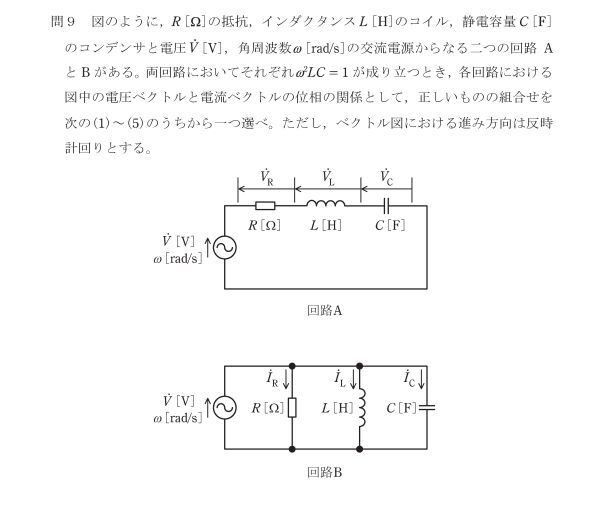
図のように、直列、並列回路があり、ともにRの抵抗、Cのコンデンサ、Lのコイルが接続されています。
この回路にて、「ω^2×LC=1」が成立する場合の、図中のベクトルの位相関係を求めよという問題です。
ここで重要なのが「ω^2×LC=1」になります。
これを分解すれば、
ω×ω×LC=1
となります。
つまり、置き換えてみれば、
2πfL=1÷2πfC(直列共振)
1÷2πfL=2πfC(並列共振)
が成り立つのです。もうこれが答えのようなものですね。
直列回路のベクトル
設問にある通り、「ω^2×LC=1」であるため、前途したように直列共振の式に変換させる事が出来ます。
2πfL=1÷2πfC(直列共振)
CとLが共振状態とみなせるので、ベクトルとしては電源電圧VとVRが同相となります。
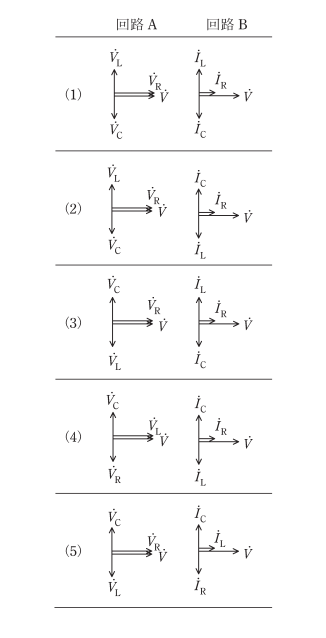
また、VLは電源Vに比べて90°進みの電圧となり、VCは90°遅れの電圧となるので、回答郡の(1)(2)に絞られます。
並列回路のベクトル
設問にある通り、「ω^2×LC=1」であるため、前途したように並列共振の式に変換させる事が出来ます。
1÷2πfL=2πfC(並列共振)
CとLが共振状態とみなせるので、ベクトルとしては電源電圧VとIRが同相となります。
また、ILは電源Vに比べて90°遅れの電流となり、VCは90°進みの電流となるので、回答郡の(2)が正解となります。


