直流回路のボーナス問題です。これを落とした方はかなり少ないと思われますが、一応解き方についてまとめてみようと思います。
抵抗のみの直、並列回路で、各抵抗で消費される電力を求める問題となります。
令和2年 理論問6
直流回路の消費電力計算問題
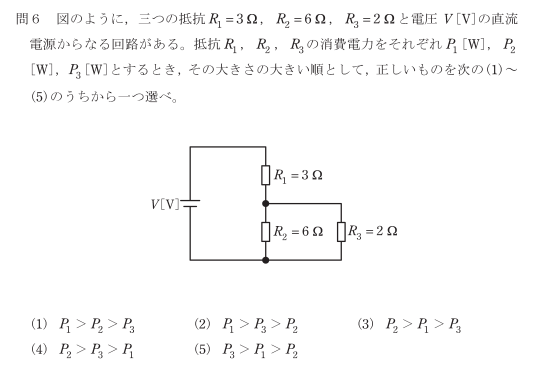
図のR1、R2、R3で消費される電力を求め、大きい順に並んでいる回答を選ぶ問題です。
各抵抗値があらかじめ記載されているので、合成抵抗Zが簡単に求めることができます。
合成抵抗Zを求める
並列を合成してから、直列を合成すればZが求まります。
Z=3+6×2/6+2=4.5(Ω)
電流値Iを求める
直流電源EはV(V)となっているので、回路に流れる電流値は
V/4.5(A)≒0.222V(A)
となります。
電圧降下を求める
回路全体に流れる電流値が0.222V(A)なので、R1にかかる電圧が求まります。
3×0.222V=0.66666V(V)
したがって、残りの並列回路に加わる電圧は、
V-0.66666V=0.333V(V)
となります。
したがって、各抵抗に流れる電流値が求まります。
各抵抗の消費電力を求める
消費電力は
VI(W)
I^2R(W)
で求まるので、これのどちらかを使って各抵抗に当てはめていきます。
今回はVIを使います。
R1(3Ω)には0.222V(A)流れるので、
0.666V×0.222V≒0.148V^2(W)・・・R1の消費電力
R2には0.33Vかかっているので、電流値は
≒0.0555V(A)
したがって
0.0555V×0.333V≒0.018V^2(W)・・・R2の消費電力
R3には0.33Vかかっているので、電流値は
≒0.1665V(A)
したがって
0.1665V×0.333V≒0.055V^2(W)・・・R3の消費電力
消費電力の大きさ順に並べると
R1>R3>R2
となり、答えは(2)になります。


