令和3年度、法規のB問題になります。昨年とは異なり、「これぞ法規のB問題!」という支線の問題が出題されました。
今年の法規B問題はこういった割とポピュラーな計算問題が全体的に出題された印象を受けましたので、事前に過去問で計算問題の対策をしていたかたは楽勝だったんじゃないかなと思います。
昨年はまさかの法律穴埋め問題でしたからね、、裏をかかれて心の中で発狂された方は私だけじゃないはず。。
ということで、今回は令和3年度、法規B問題の問11「支線に生じる引張荷重、最小素線条数の計算問題」を解説しようかと思います。
令和3年 電検三種「法規問11」
(a)問題 支線に生じる引張荷重を求めよ
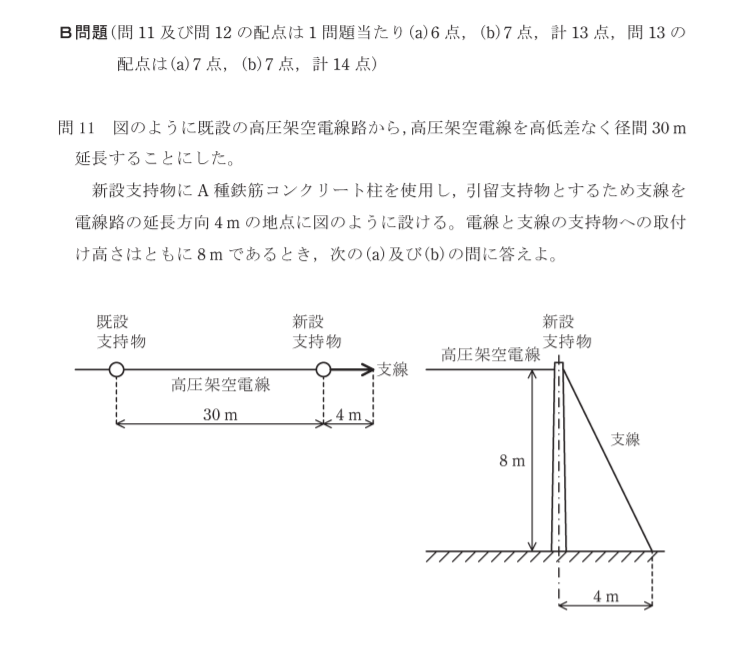

電線の水平張力が15kNと設問にあるので、これを支線で打ち消してやればいい事がわかります。
電線は1本で支線は電線と同じ高さにあるため、水平張力に高さを加味する必要はありません。とりあえず電柱8mの位置から電線の逆方向に、水平に15kNの線を短く仮で引いてやります。
そこから直下に、支線と交わるまで線を引きます。これで出来た直角三角形は、支線の長さ(比率)を表す三角形になります。
図から支線の長さは、√8^2+4^2≒8.944 となります。
したがって三角形の比率は、縦1:横2:斜め2.236 となります。
これを水平張力に置き換えてやれば、水平に描いた15kNは縦の成分になるので、これを元に斜め成分を出してやれば、支線に生じる引張荷重の値が求まります。
縦1:横2:斜め2.236 なので、縦成分を2.236倍したものが答えとなります。
15kN×2.236=33.54kN
「支線に生じる引張荷重としてもっとも近いものを選べ」とあるので、33.54kN以上の近似値である「34kN」が答えとなります。
したがって、回答群(4)が正解になります。
(b)問題 支線の最小素数条数を求めよ

先ほど求めた支線の引張荷重を元に、支線に必要な最小素線条数を求める問題です。
こちらは公式を知っていれば簡単ですね。
素線1本あたりの引張強さは、
素線の面の半径^2×π×より線の引張強さ
になります。
したがって、設問の場合の素線1本あたりの引張強さは、
1.45^2×π×1.23kN≒8.12kN
となります。
後は先ほど求めた支線にかかる引張荷重をこの値で割ってやればいいのですが、設問には「安全率が1.5」とありますので、支線にかかる引張荷重に1.5をかける必要があります。
よって、次式で必要な素線条数が導け出せます。
34kN×1.5/8.12kN≒6.27
6.27本以上の素線条数が必要なので、回答群(3)の7 が正解となります。