令和3年度電検三種、法規の問13になります。
B問題としては王道中の王道問題だと思いますので、はっきりいってボーナス問題だったと思います。本当に昨年の法律穴埋めB問題と比べれば、今年は超イージーになった年だとつくづく思いますね。。
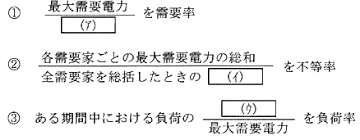
需要率、負荷率、不等率、の公式さえ頭に入っていれば、難なく解ける問題です。
来年の法規、怖いですね。。
それでは、今回はこの問題を解説しようかと思います。
令和3年 電検三種「法規問13」
(a)問題 総需要電力量を求めよ
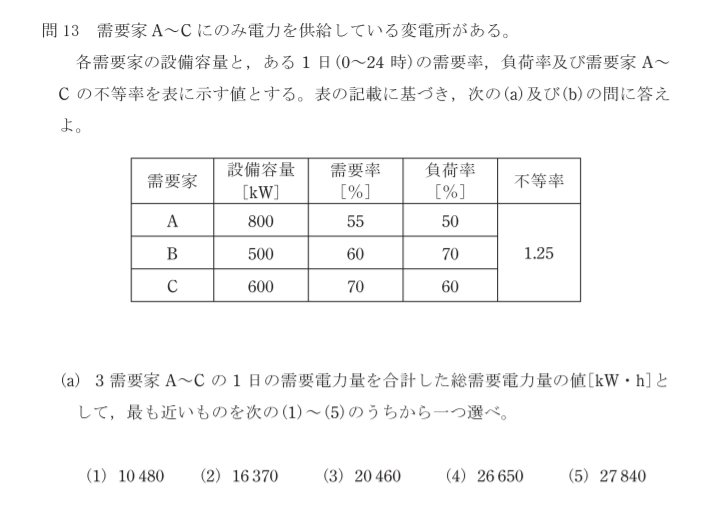
設問内容から、A~Cの需要家それぞれの平均電力を求め、「1日」とあるので、×24してA~Cを足せば答えが求まります。
平均電力を求めるには、
負荷率=平均電力/最大需要電力 × 100
の公式を使えばいいので、設問の表から、あとは「最大需要電力」が分かれば各需要家の平均電力が求まります。(負荷率がすでに求まっているため。)
最大需要電力は、
需要率=最大需要電力/設備容量 × 100
の公式で求める事ができるので、設問の表からすでに求まっている「需要率」「設備容量」を利用すると各需要家の最大需要電力が求まります。
公式を展開すると、
最大需要電力=需要率(%)×設備容量/100
になるので、
Aの最大需要電力:55×800k/100 = 440KW
Bの最大需要電力:60×500k/100 = 300KW
Cの最大需要電力:70×600k/100 = 420KW
となります。
続いて、各需要家の平均電力を求めます。
公式を展開すると、
平均電力=最大需要電力×負荷率(%)/100
になるので、
Aの平均電力:440k×50/100 = 220KW
Bの平均電力:300k×70/100 = 210KW
Aの平均電力:420k×60/100 = 252KW
となります。
あとはこれに24Hをかけて、足せば答えが求まります。
220k×24+210k×24+252k×24=16368KW・H
回答群より、最も近いのは(2)の16370KW・H になります。
(b)問題 総合負荷率の値を求めよ

設問aにて、各需要家の最大需要電力と平均電力が求まったので、負荷率を求める公式を使えば、総合負荷率の値を求めることができます。
負荷率を求める公式は、
負荷率=平均電力/最大需要電力 × 100
になります。
これを「総合負荷率」に変換する場合は、平均電力にA~Cの平均電力の合計を、最大需要電力にA~Cの最大需要電力の合計を代入してやればOKです。
総合負荷率=220k+210k+252k/440k+300k+420k × 100 ≒ 58.7%
回答群から、一番近いのは(2)の59% となります。