法規B問題で出題される傾向にあるの1つに「支線に生じる引張荷重と支線の条数の求め方」があります。
過去10年でも3回程?はあったような気がします。
比較的簡単な計算ですむ問題ですが、少し引っ掛けてくる内容も含まれています。
今回はその「引っ掛け」てくる要素も考慮した問題の解き方についてまとめてみます。
平成16年 問11
支線に生じる引張荷重の求め方
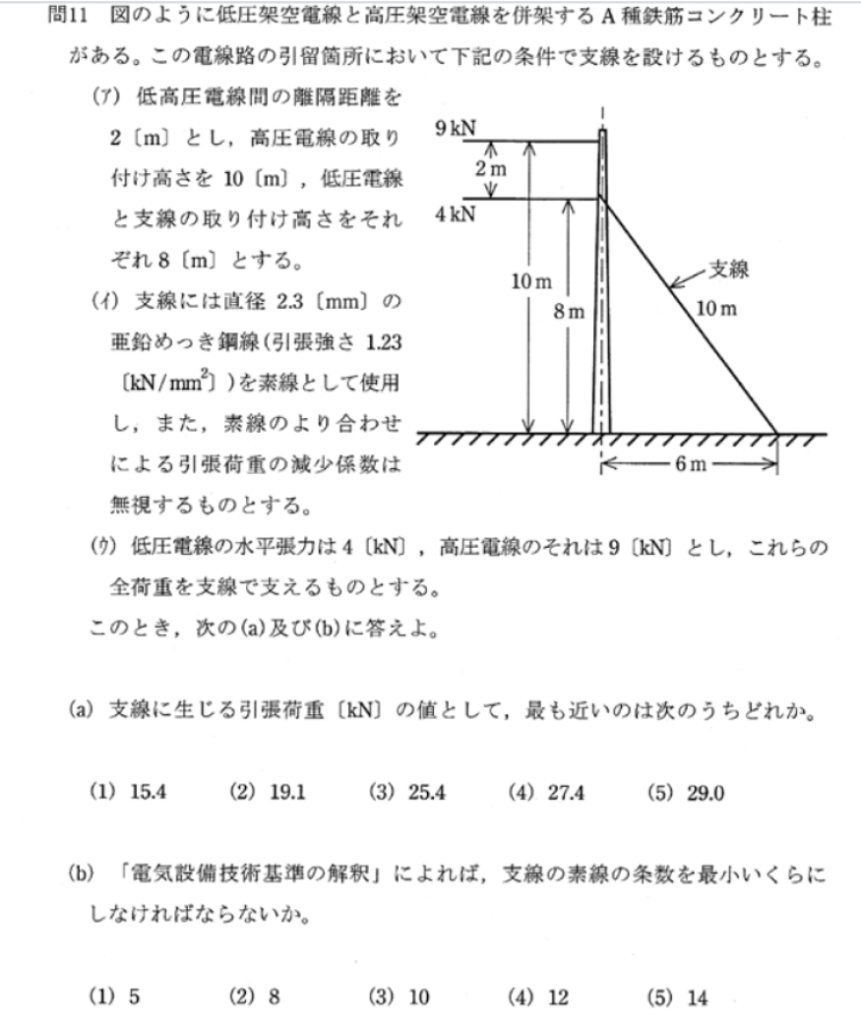
問題文の通り、電柱に低圧と高圧の電線(図の左側)が取り付けられており、それを支線(右側)の1本で支えている形になります。
これは電線の引張荷重(引っ張られる力)によって電柱が倒れる事を防ぐ目的で「支線」が張られているわけです。
つまり、電線の引張荷重と同じ引張荷重を、支線が反対方向に張る事が出来れば、電柱の均衡が取れるという事です。
電線側の引張荷重を求める
したがって、まずは「電線側の引張荷重」を求めます。次式のように、「高さ×引張荷重」で求まります。
高圧電線:10(m)×9(KN)=90(KN)
低圧電線:8(m)×4(KN)=32(KN)
高圧と低圧の2つの電線があるので、それぞれの引張荷重の値が出れば、それを足します。
90(KN)+32(KN)=122(KN)
これが電線側の引張荷重になります。
気を付けたいのは、今回のように電線と支線が直線で結ばれていればこの計算で問題ないですが、支線に対して角度が生じた場合、それを加味した引張荷重を算出することが必須になります。
ベクトルの合成が必要になるって事です。
支線の引張荷重の求め方
支線には高さの反対方向、図でいうと8mから右方向に「122KN」の引張荷重をかければよくなりますが、支線はナナメになっている為、ベクトルの計算が必要になります。
一先ず、右方向に適当な長さの直線を引き、それを122KNに該当する高さ8mで割った数「15.25KN」とします。
そこから垂直に下へ線を引き、支線と交わる点が「支線の引張荷重」の値になります。
支線を見ると、縦、横、斜め、の長さが分かっているので、3:4:5の三角形になっている事が分かります。
つまり、横成分が15.25KNになるので、支線の引張荷重となる斜め成分は、約「25.4KN」となります。
答えは(3)になります。
支線の素数の条数の求め方
素線の引張強さを求める
支線は問題文にある通り、複数の「素線」をより合わせたもので成り立っています。
今回の場合は「亜鉛メッキ銅線」であり、「引張強さ1.23KNmm^2」とあるのでそのまま引張強さを「1.23KN」と考えがちですが、「1.23KNmm^2」です。
つまり、「素線の面積×引張強さ1.23KNmm^2」が引っ張り強さになりますので、問題文にある「直径2.3mm」を考慮しなければなりません。
したがって、素線の引張強さは、
(2.3×0.5)^2(半径×半径)×3.14(π)×1.23(KN)≒5.11KN
となります。
引張荷重の減少係数と安全率を考慮
後は、支線の引張荷重「25.4KN」を素線の引張荷重「5.11KN」で割れば答えが出そうですが、ここが引っ掛けで「引張荷重の減少係数と安全率」を考慮しなければなりません。
引張荷重の減少係数は、素線の引張荷重に掛けてやらなければなりません。ただし、今回のように指定がなければそのままで問題はありません。
安全率は、今回指定はありませんが、いやらしい事に、支線の条数を決める問の文章に「電気設備技術基準の解釈によれば」と記載があります。
つまり、安全率も考慮しなくてはなりません。
安全率は基本「2.5」とされていますが、A種鉄筋コンクリート柱で全電線の引張荷重を支線で支える場合は「1.5」となります。
したがって、今回の安全率は「1.5」が適用されます。
そして、安全率は、「支線に生じる引張荷重」に掛ける事になります。
ですので、
「25.4KN×1.5」が、安全率を加味した支線に生じる引張荷重になります。
支線の素数の条数を求める
まとめると次式になります。
25.4KN(支線に生じる引張荷重)×1.5(安全率)÷5.11KN(素線の面積×引張強さ×減少係数)≒7.45
つまり、7.45本以上が答えになります。
したがって答えは(2)の8本になります。