直流機のしくみ
直流の電気を作る「直流発電機」や直流によって動力を発生する「直流電動機(直流モーター)」を、まとめて「直流機」といいます。
直流発電機の原理
図のように磁界のなかで長方形のコイルを回転させるとコイルの両辺に起電力が誘導されます。
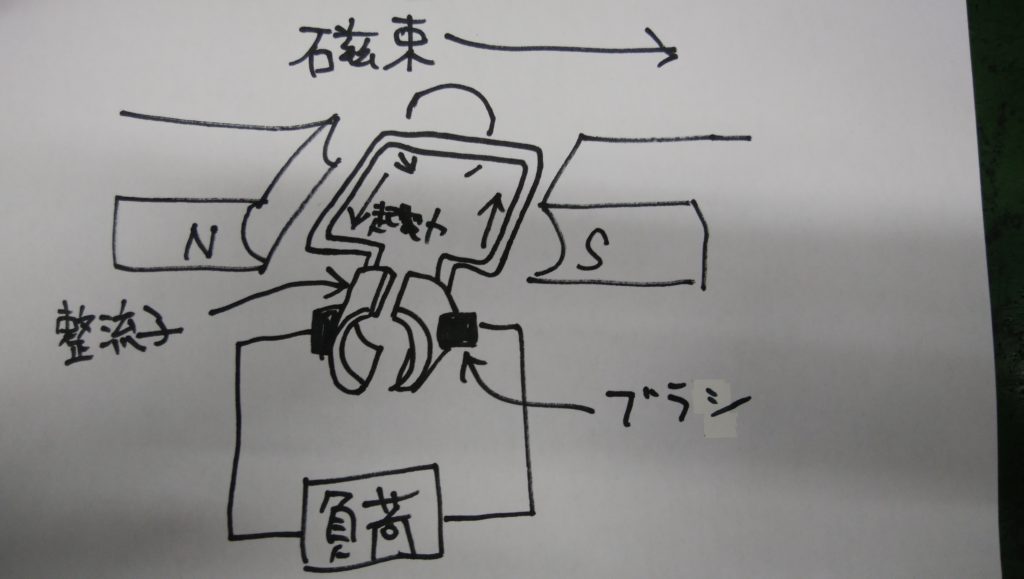
コイルの両辺に誘導される起電力の向きは「フレミング右手の法則」にしたがうのでコイルが半週するごとに逆向きになります。
したがってコイルの両端からこの起電力をそのまま取り出すと交流を作る同期発電機になります。
一方、直流発電機ではコイルの両端に「整流子」と呼ばれる半円形の金属片を取り付け、「ブラシ」とよばれる端子と接触させます。
下図のように整流子はコイルと一緒に回転します。コイルが半回転して電流の向きが変わるとブラシに接触した整流子も入れ替わるため、
ブラシには常に同じ方向の電流が流れるしくみになっています。
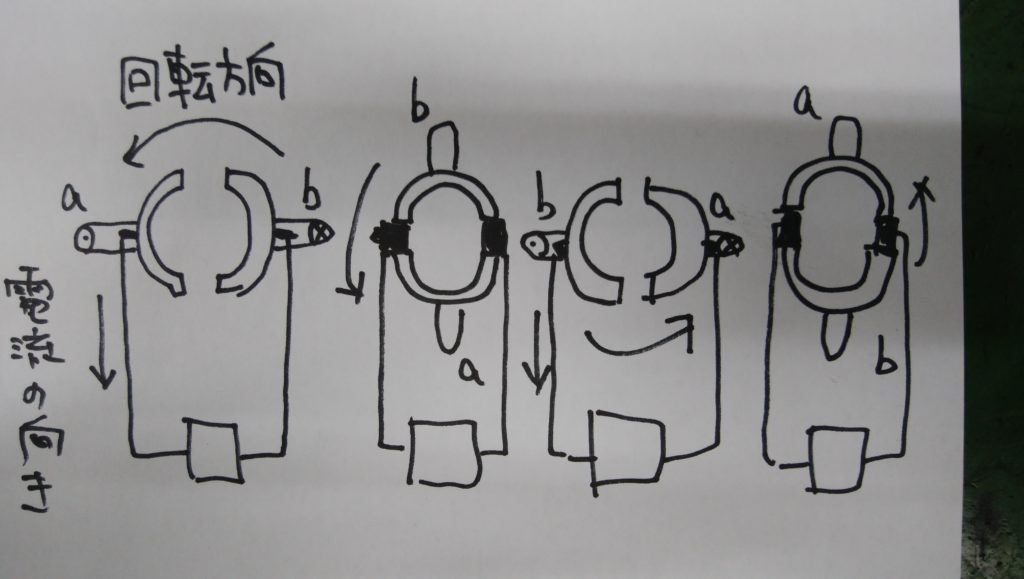
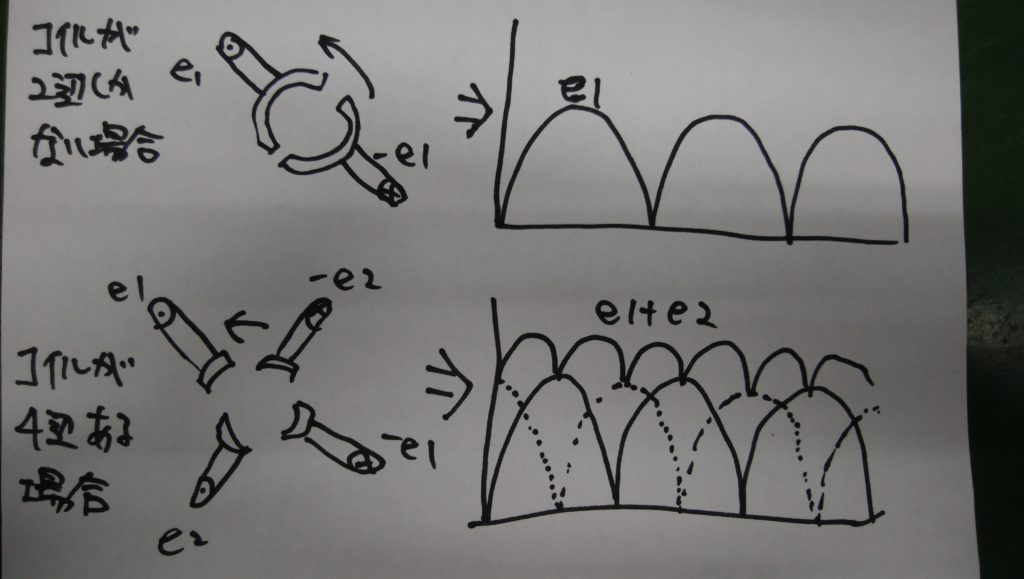
ただし、コイルが2辺しかないと図のように脈動の激しい電気になってしまうので、実際の発電機ではコイル辺をたくさん設けて、より直流に近い電気をつくります。
直流電動機は左手の法則にしたがう
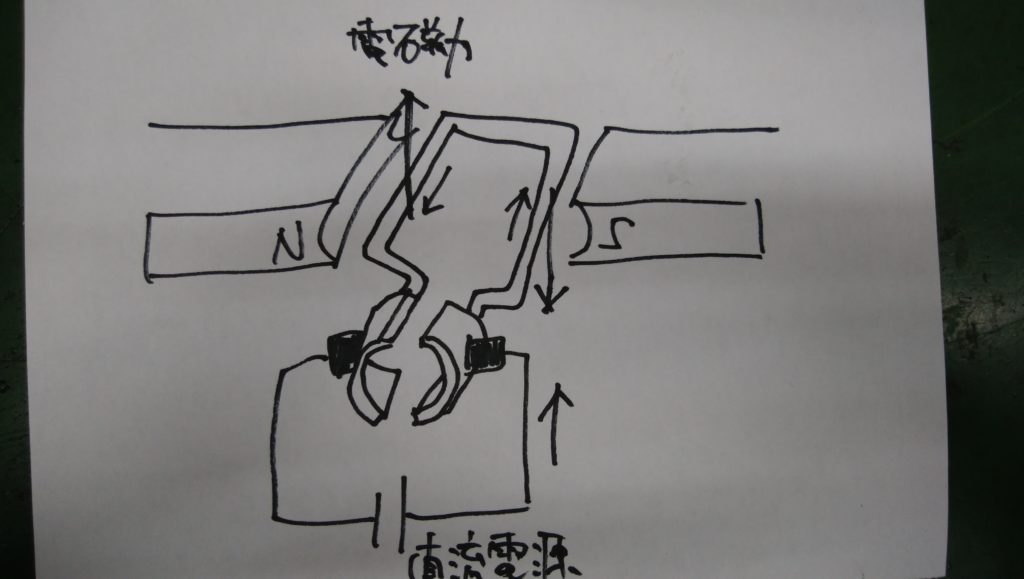
直流電動機は、直流発電機の負荷の代わりに直流電源を接続したものです。
コイルの両辺には「フレミングの左手の法則」にしたがう電磁力が作用し回転力が生まれます。
直流機の構造
直流機の構成要素
直流機の部品は大きく「回転子」と「固定子」に分かれます。
回転子:回転する部品(電機子、整流子など)
固定子:固定されている部品(界磁、ブラシなど)
電機子
実際の直流機では磁束を通りやすくするため磁極間に円筒形の鉄心が置かれます。また、コイルは鉄心の表面にある「スロット」(切り込み)のなかに収納され、鉄心ごと回転するようになっています。
鉄心とコイルを組み合わせた装置を「電気子」といいます。また、円筒形の鉄心を「電機子鉄心」、コイルを「電機子巻線」といいます。
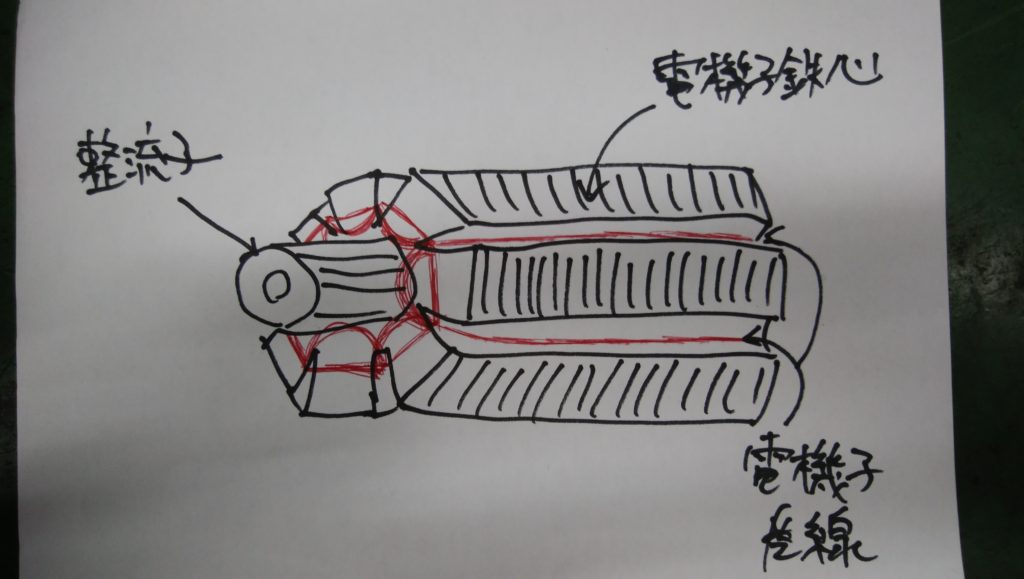
界磁
磁束をつくるための磁極はふつう永久磁石ではなく鉄心に巻線を巻いたもので、「界磁」といいます。界磁の鉄心と巻線をそれぞれ界磁鉄心、界磁巻線といいます。
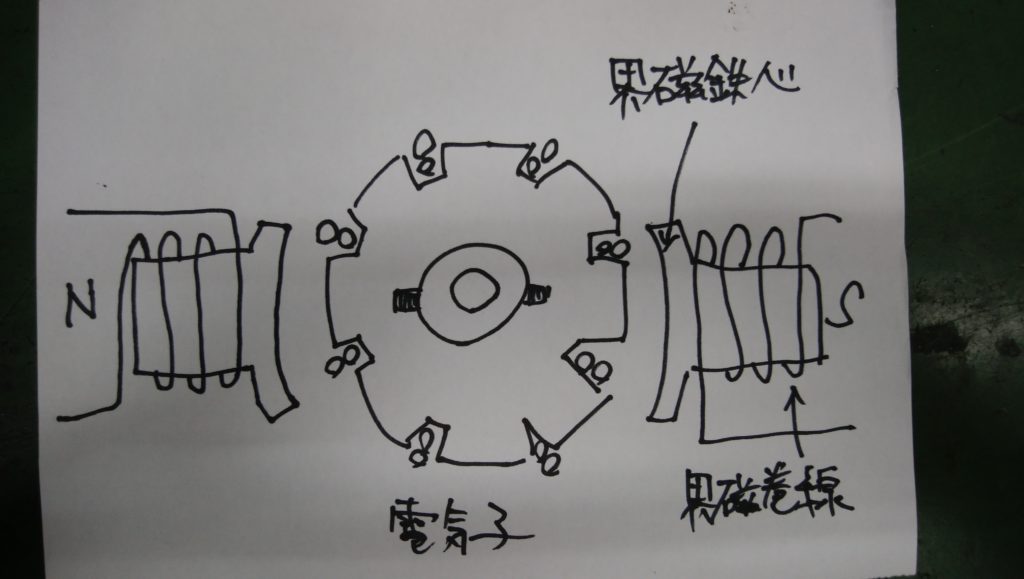
励磁方式による直流機の分類
界磁鉄心は界磁巻線に電流が流れる事で磁化されます。直流電動機や発電機は界磁をどのように磁化するかによって次のような種類に分類されます。
他励式
界磁巻線の励磁電流を電機子とは別の電源から取る方式
直巻式
界磁巻線と電機子とを直列に接続する方式
分巻式
界磁巻線と電機子とを並列に接続する方式
複巻線
直巻と分巻の両方をもつ方式
電機子反作用の対策
電機子反作用とは
電機子巻線に電流が流れるとこの電流による磁界が生じ、界磁がつくる主磁束に影響を与えます。
この現象を「電機子反作用」といいます。
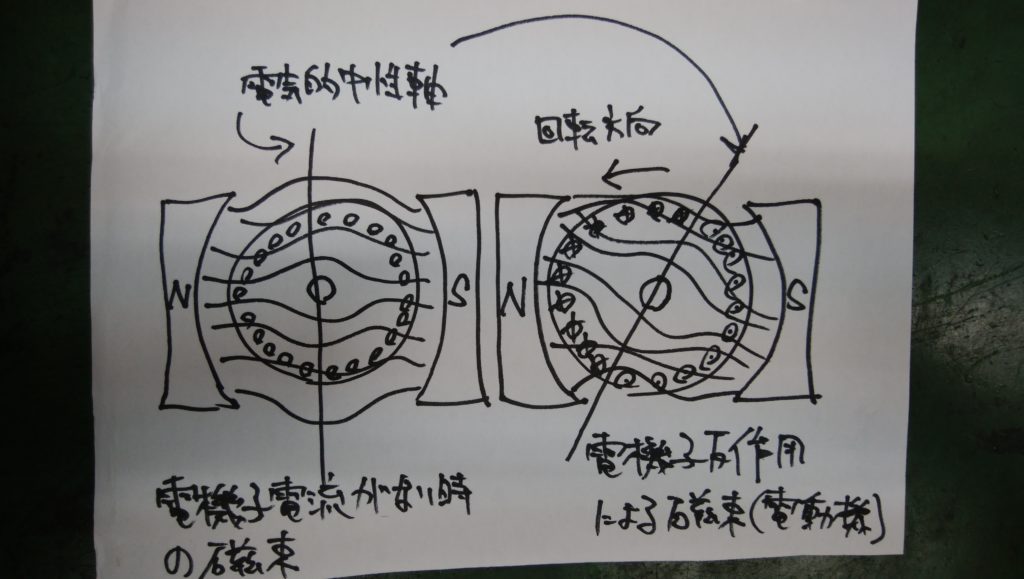
電機子反作用による問題点
電機子反作用が生じると直流機に以下のような問題が生じます。
・整流の悪化:電気的中性軸が移動するため整流が正しく行われなくなります。
・主磁束の減少:鉄心の磁化飽和により磁束が減少します。
・整流子片間に火花発生:整流子片間に電圧が不均一になり火花やフラッシオーバーが発生しやすくなります。
電機子反作用を防止するには
電機子反作用への対策として、直流機には「補極」や「補償巻線」が設置されています。
補極
主磁極の間に設置する磁極。電気的中性軸の移動を防ぎ整流を改善します。
補償巻線
電機子電流による起磁力を打ち消すため、磁極片の表面に取り付けて電気子電流と逆向きの電流が流れるようにした巻線。
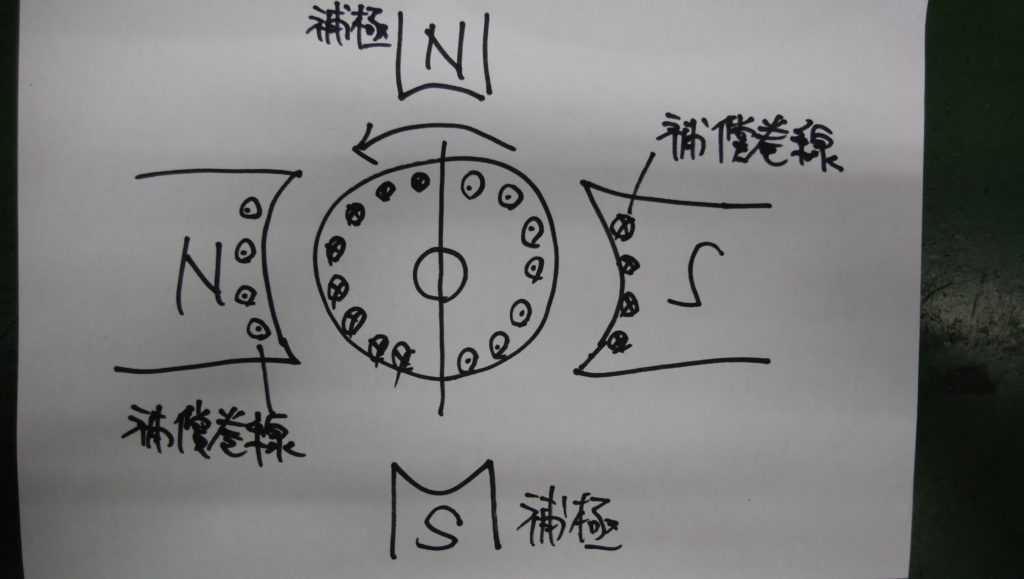
電機子巻線の巻線方法
重ね巻と波巻
電機子巻線の巻き方には「重ね巻」と「波巻」の2種類があります。巻線方式は、電動機ではトルクに、発電機の場合は誘電起電力に影響を与えるので、違いを把握しおておきましょう。
重ね巻
重ね巻は下図の展開図のようにコイル辺を1本ずつずらしながらスロットに収めていく巻き方です。
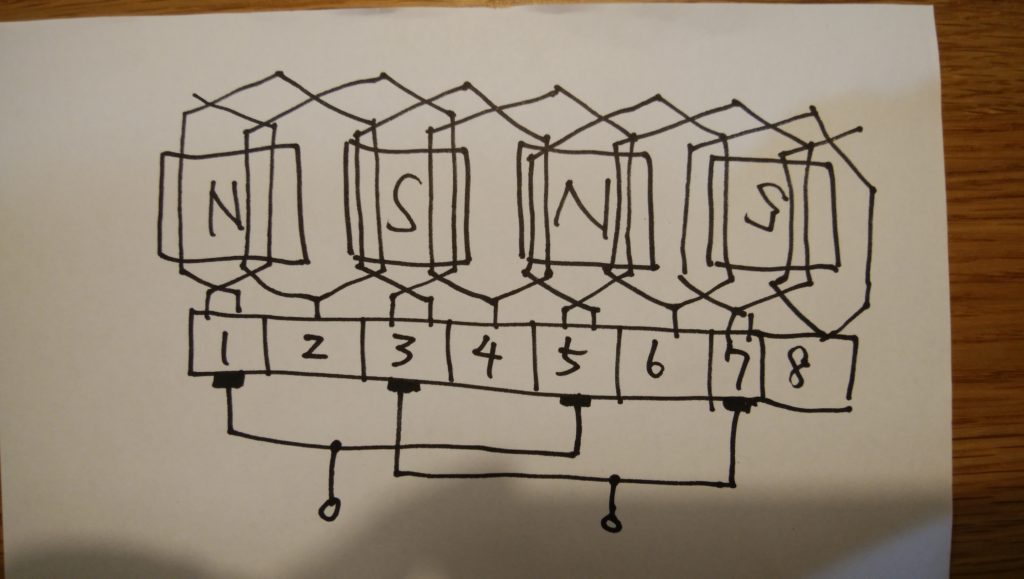
・磁極と同数の回路を並列に接続する。
・磁極と同数のブラシがある。
・並列回路が多くなる場合は、「均圧結線」が必要。
波巻
波巻は1回路のコイル辺が全スロットに収まるように、波巻に巻いていく巻き方です。
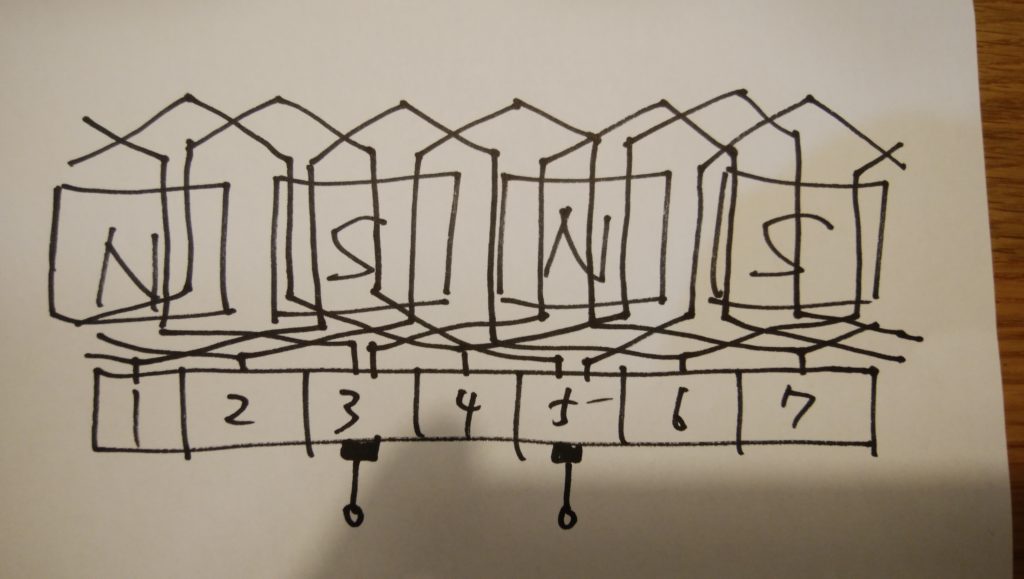
・並列回路は磁極数にかかわらず2。
・ブラシの数は磁極数にかかわらず2。
電機子巻線の並列回路
電機子巻線を延ばしてみるとコイル辺を直列につないだ回路が図のように並列に接続されていることがわかります。
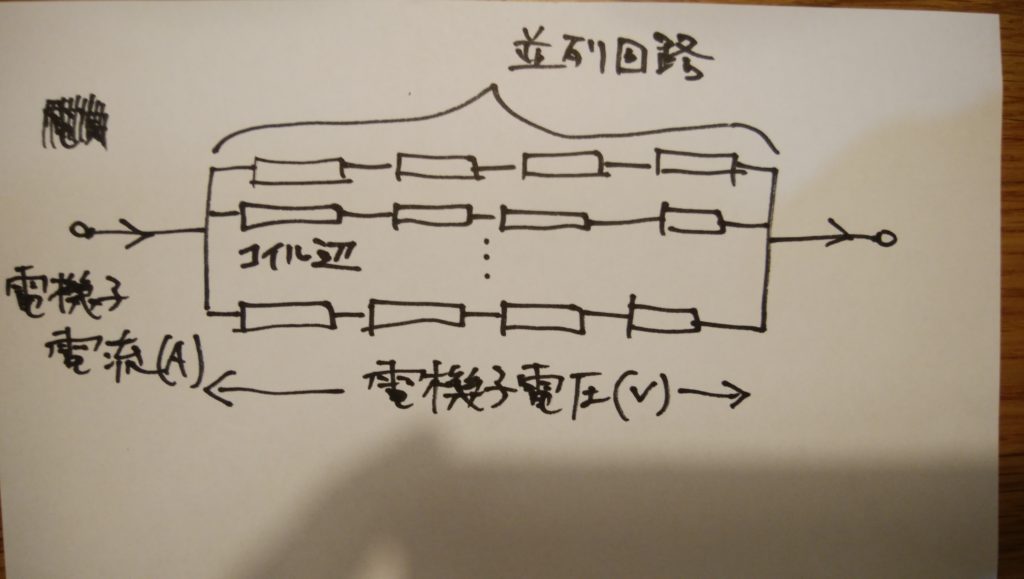
したがって電機子全体の誘導起電力と電流はそれぞれ次のように計算できます。
電機子全体の誘電起電力=コイル1辺の誘導起電力×コイル総数/並列回路数(V)
電機子電流=コイル電流×並列回路数(A)
並列回路の数は重ね巻の場合は磁極数と等しく波巻の場合は磁極数にかかわらず2本です。
そのため一般に電機子全体の誘導起電力は波巻のほうが大きく、電機子電流は重ね巻の方が大きくなります。
直流発電機の誘導起電力
発電機の誘導起電力を計算する
長さl(m)の導体が磁束密度B(T)の磁界磁を速さv(m/s)で切る時の誘導起電力eはの式で求められます。
e=Blv(V) ※2020/6/16修正
発電機の場合は導体(コイル辺)が回転するので速さv(m/s)の代わりに回転速度(一分間当たりの回転数。Min^-1)を使って計算します。
電機子の回転速度と導体の速さはつぎの式で表されます。
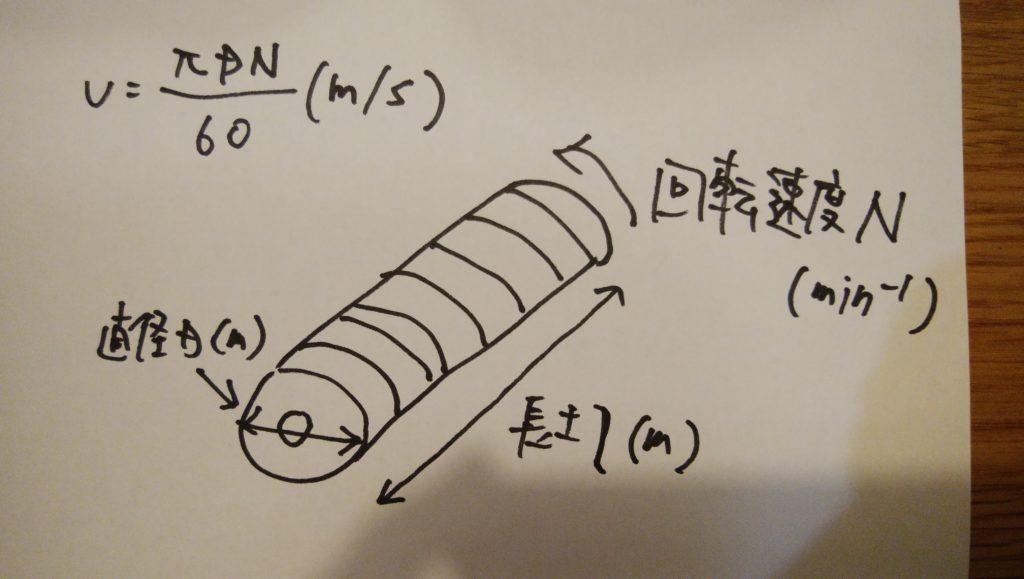
また磁束密度はもともと単位面積当たりの磁束ですから磁極数をp、1極の磁束をΦ(Wb)とすれば電気子を通る磁束密度Bは次のように求められます。
B=pΦ/πDN(T)
以上より電気子の導体一本当たりの誘導起電力はつぎのように求められます。
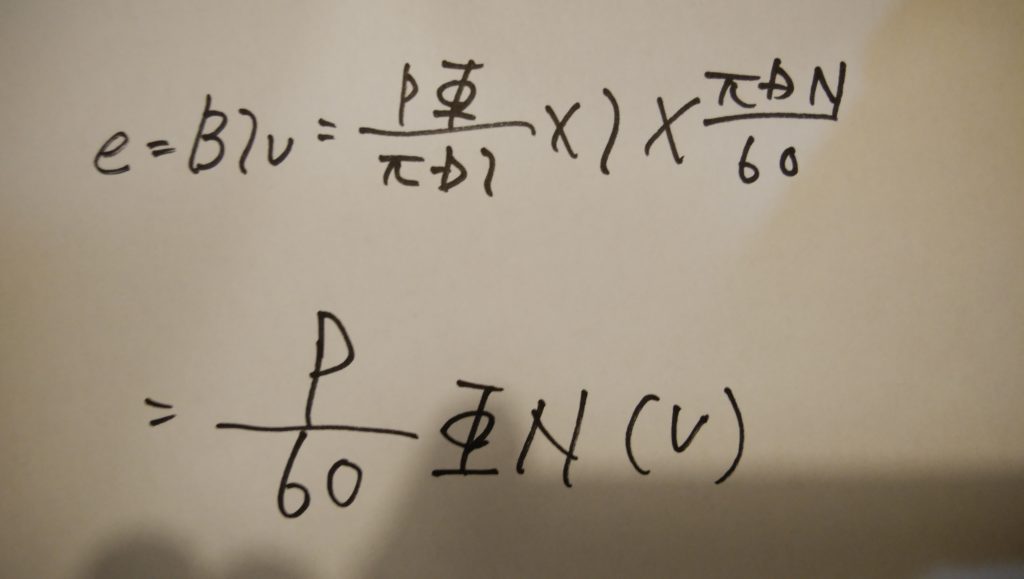
電機子の導体数をz、電気子巻線の並列回路数をαとすると電気子全体の誘導起電力Eは上式のz/α倍になります。すなわち

端子電圧と負荷電流
直流発電機の端子電圧は電気子で誘導された起電力から発電機の特性によって生じる電圧降下を差し引いたものです。
電圧降下には次のような種類があります。
・電気子巻線がもつ抵抗による電圧降下
・電機子反作用による電圧降下
・ブラシの接触抵抗による電圧降下
・界磁巻線がもつ抵抗による電圧降下
端子電圧V(V)と電圧降下の関係は発電機の励磁方式によって異なり、次のような式で表せます。
直巻式の端子電圧
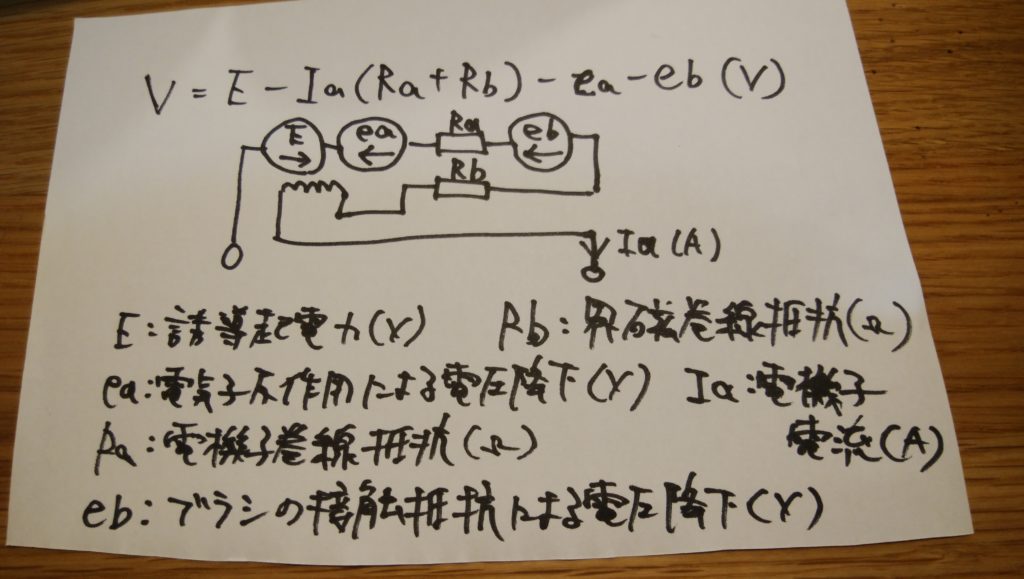
分巻式(他励式)の端子電圧
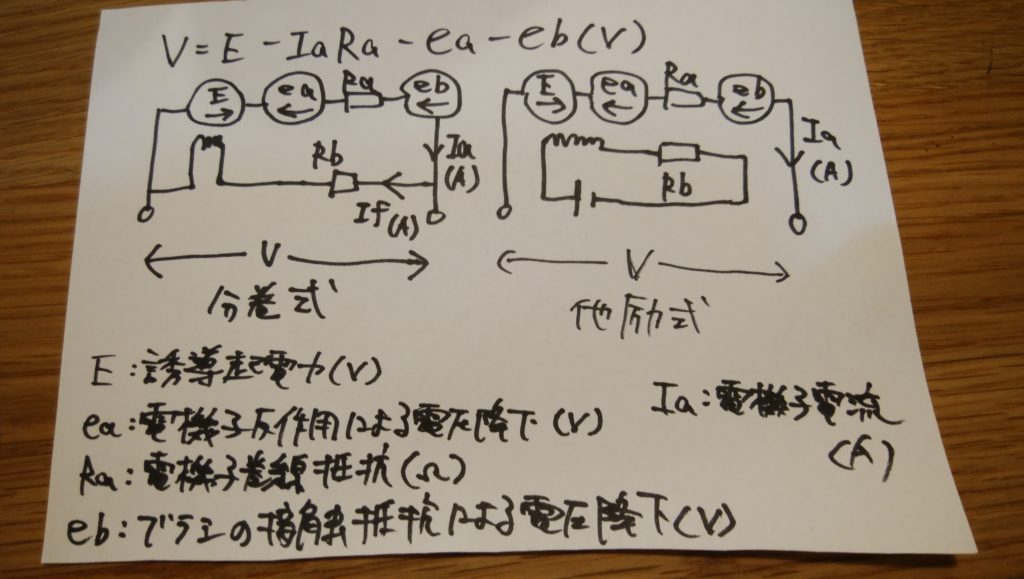
端子電圧V(V)の直流発電機に負荷R(Ω)を接続すると、オームの法則によりV/R(A)の大きさの「負荷電流」が流れます。
この負荷電流をIとすれば、直流発電機の出力P(W)は次のように求めることができます。
P=VI=I^2R(W)
電機子巻線に電気子電流が流れると電気子巻線に電磁力が生じます。この電磁力の向きはフレミングの左手の法則にしたがうため、発電機の回転と逆方向になります。
回転速度を保つにはこの電磁力に打ち勝つだけの回転力を電機子に与える必要があります。
直流電動機のトルクと回転速度
電動機が回転する力を「トルク」といいます。トルクは回転軸からの距離と電機子に加わる力の積で表され、単位にはN・m(ニュートン・メートル)が用いられます。
直流電動機のトルクを計算する
磁束密度B(T)の磁界のなかに長さl(m)の導体を置き、I(A)の電流を流したとき、導体に作用する電磁力の大きさF(N)は次式で表されます。
F=BlI(N)
電機子のコイル辺の総数をz本とすれば電気子全体に働く電磁力は
Fz=BlIz(N)
また、電気子を通る磁束の磁束密度はB=pΦ/πDN(T)ですから、電動機の電気子のトルクT(N・m)は次のように求められます。

電動機の逆起電力と回転速度の関係
ty区流電動機が回転すると、電気子巻線が磁束を切るので起電力が誘導されます。この起電力を「逆起電力」といいます。
逆起電力E(V)の向きはフレミング右手の法則にしたがうので、電気子電流Ia(V)と逆方向になります。そのため電動機が回転を続けるには逆起電力に打ち勝つだけの端子電圧V(V)を加える必要があります。電気子巻線の抵抗をRa(Ω)とすればこれらの関係は次の式で表せます。
Ia=V-E/Ra(A) ⇒ V=E+IaRa(V)
また逆起電力Eの大きさは回転速度をN(min^-1)磁束をΦ(wb)とすれば次のように求めることができます。
E=k1ΦN(V)
上記より、電動機の回転速度Nは次の式で表されます。
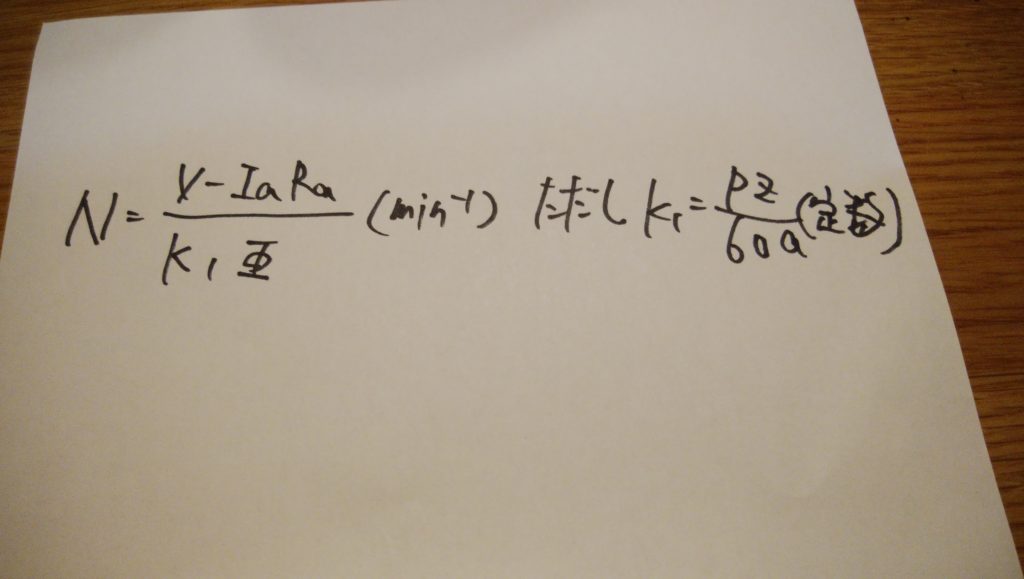
電動機の出力とトルクの関係
電機子へ入力する電力(W)は端子電圧V(V)と電機子電流Ia(A)の積ですから
Via=(E+IaRa)Ia=Eia+Ia^2Ra(W)
このうちia^2Ra(W)は電気子抵抗によって失われる損失でEia(W)が機械エネルギーに変換される電動機の出力に当たります。
以上より直流電動機の出力P(W)はつぎのようにもとめられます。

直流電動機の特性
直流電動機の回転速度と電機子電流の関係を示したグラフを「速度特性曲線」といいます。
また、直流電動機のトルクと電機子電流の関係を示したグラフは「トルク特性曲線」と呼ばれます。
分巻・他励電動機の特性
直流電動機の回転速度NとトルクTはそれぞれ次の式で表す事ができます。
N=V-IaRa/k1Φ(min^-2)
T=k2ΦIa(N・m)
分巻電動機や他励電動機では界磁電流Ifか端子電圧Vを一定とすれば界磁磁束Φは電気子電流Iaにかかわらず一定です。
そのため分巻電動機と他励電動機の特性曲線は次のようになります。
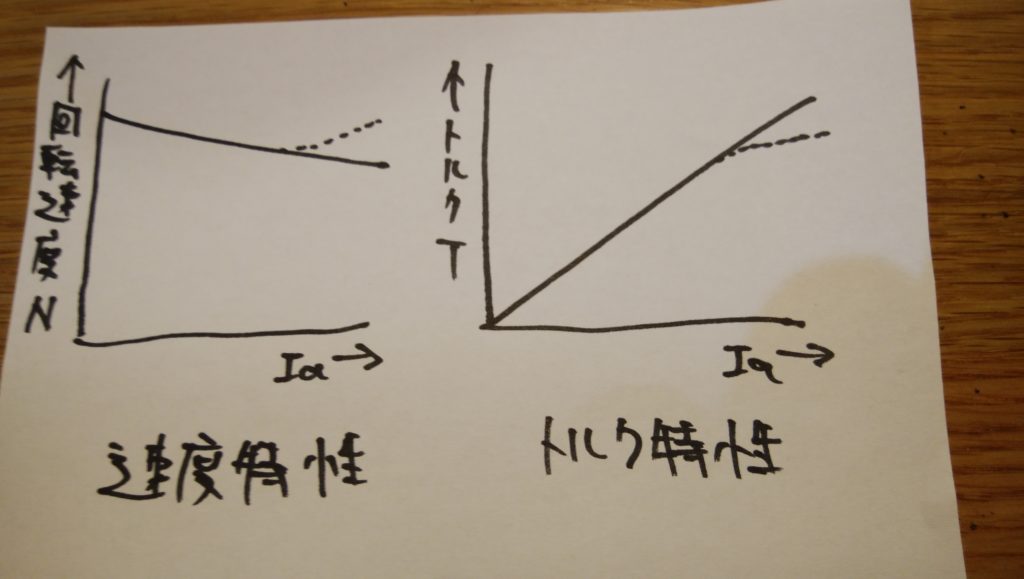
なお、電気子電流が一定以上になると4電気子反作用によって磁束が減少するため、図の点線部のように回転速度は上昇し、トルクは増加しなくなります。
直巻電動機の特性
直巻き電動機は界磁巻線と電機子が直列に接続され、電気子電流Ia=界磁電流Ifとなります。そのため
Φ=kΦIf=kΦIa(kΦは比例定数)
となり回転速度とトルクはそれぞれ次の式となります。
N=V-IaRa/k1kΦIa=V/k1kΦ×1/Ia-Ra/k1kΦ
T=k2kΦIa^2
これらの式から直流電動機の回転速度は電気子電流Iaに反比例し、トルクは電気子電流の2乗に比例することがわかります。
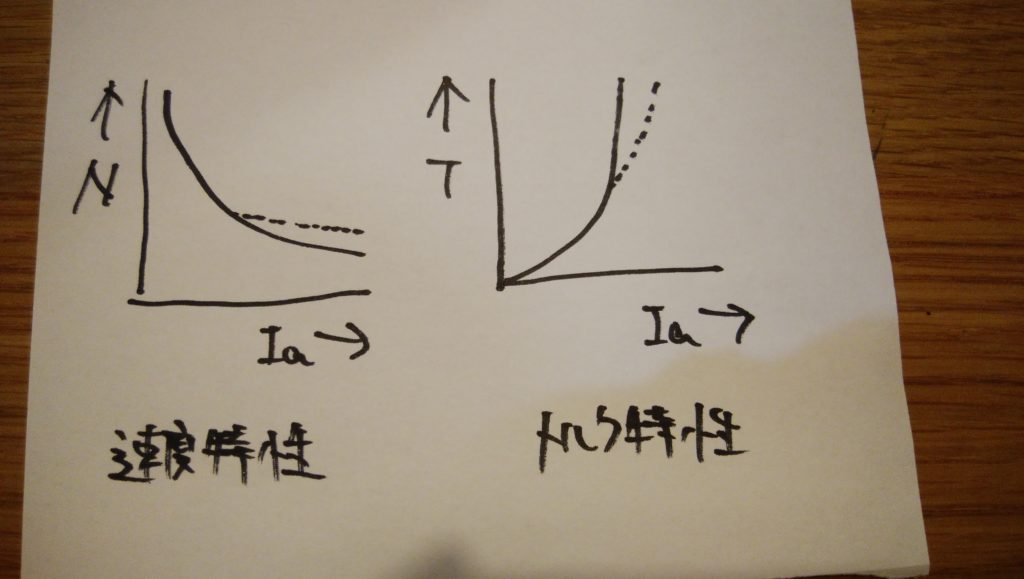
なお、電気子電流が一定以上になると界磁の磁化飽和によって磁束がそれ以上ふえなくなるため、曲線の傾きは図の点線部分のようにゆるやかになります。


こんにちは
本年9月に電験三種初挑戦を予定している世間一般でいうところの前期高齢者です。
本文中に示されている直流発電機の誘導起電力の式ですが正しくは下記右側ではないでしょうか?
e=Ble → e=Blv(V)
はじめましてトムキチさま。
ご指摘ありがとうございます。早速修正させていただきました。