目次
変圧器の基礎
変圧比と巻数比
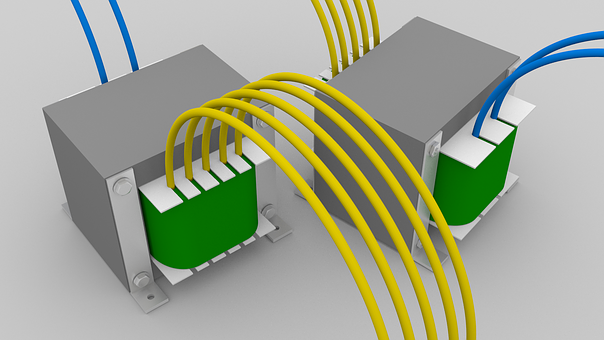
図のように変圧器の一次巻線に交流電圧V1を加えると、一次巻線n1に電流Io(A)が流れ、これによって起磁力n1Ioが生じます。
電流Ioは、鉄心の磁束を作る電流なので「励磁電流」といいます。励磁電流は、一次電圧V1から90°位相が遅れた電流です。
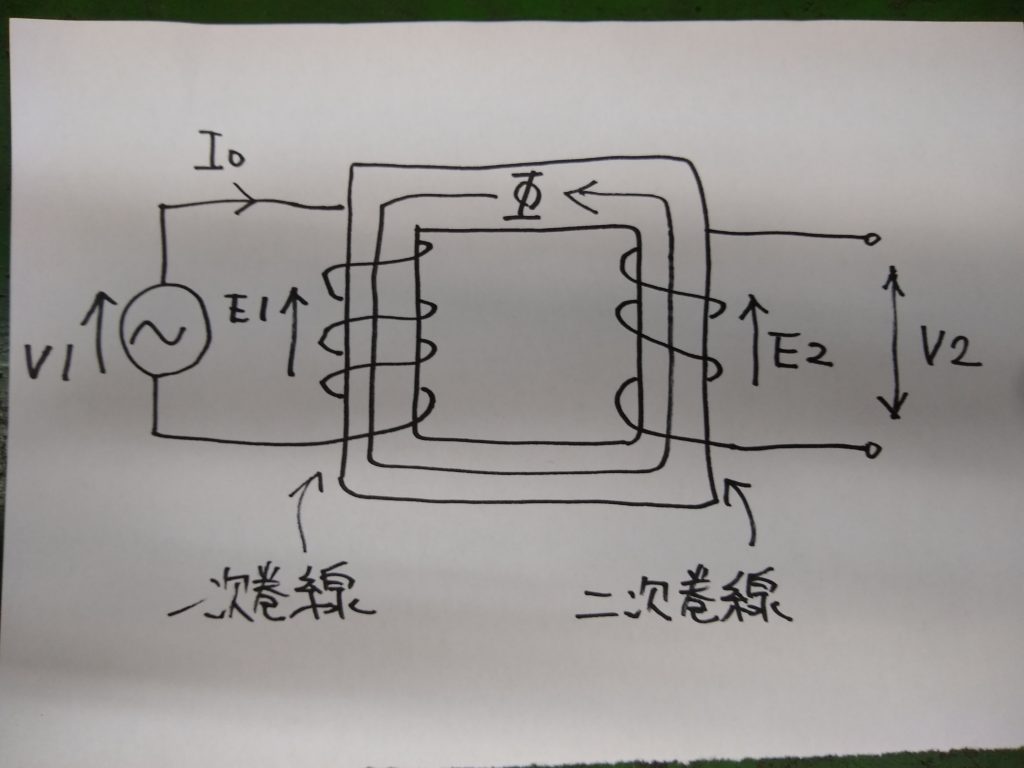
励磁電流によって鉄心には磁束Φ(wb)が発生します。磁束Φは、一次巻線と二次巻線を貫いて起電力E1、E2を誘導します。
これらの起電力はファラデーの法則により次式で表せます。
E1=-n1×ΔΦ/Δt(V)
E2=-n2×ΔΦ/Δt(V)
一次巻線に誘導される起電力E1は、交流電圧V1と大きさが等しく、方向が逆向きになります。また、二次端子電圧V2はE2と等しいので次の関係式が成り立ちます。
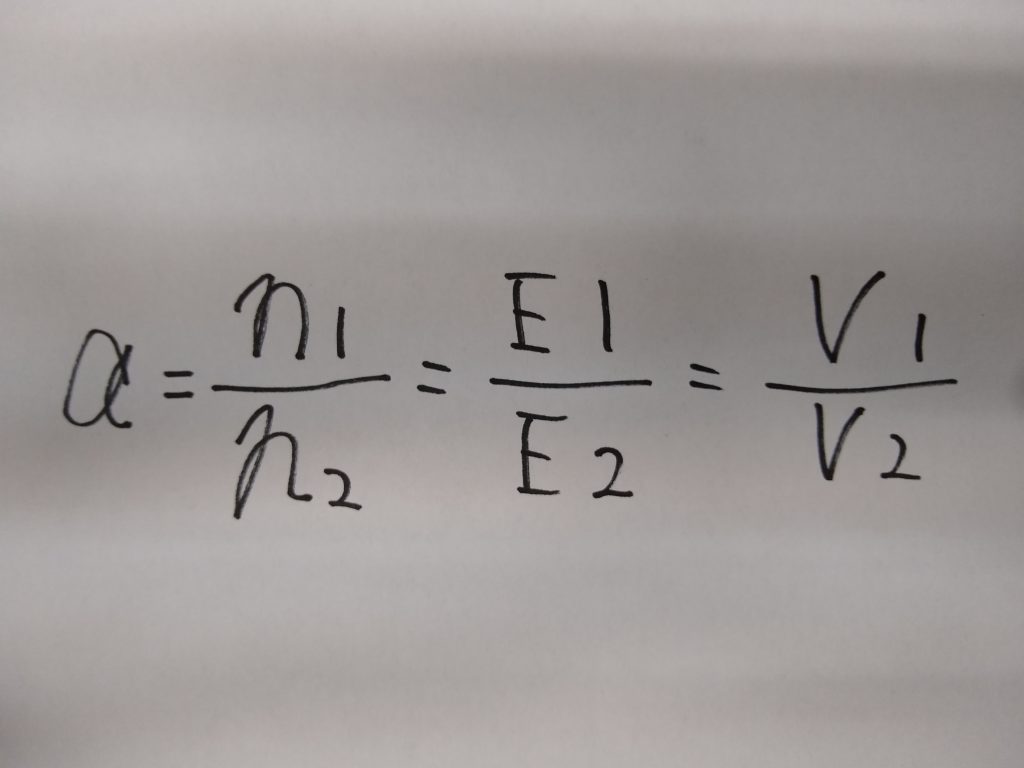
n1/n2を「巻数比」といい、V1/V2を「変圧比」といいます。すなわちこの式は変圧器の変圧比は巻数比と等しいことを表しています。
二次電流と一次電流
図のように、変圧器の二次端子に負荷を接続すると二次巻線にはE2/Zで表される電流I2が流れます。この電流を「二次電流」または「負荷電流」といいます。
負荷電流によって鉄心には起磁力n2I2が加わり、磁束Φに変化を与えようとします。
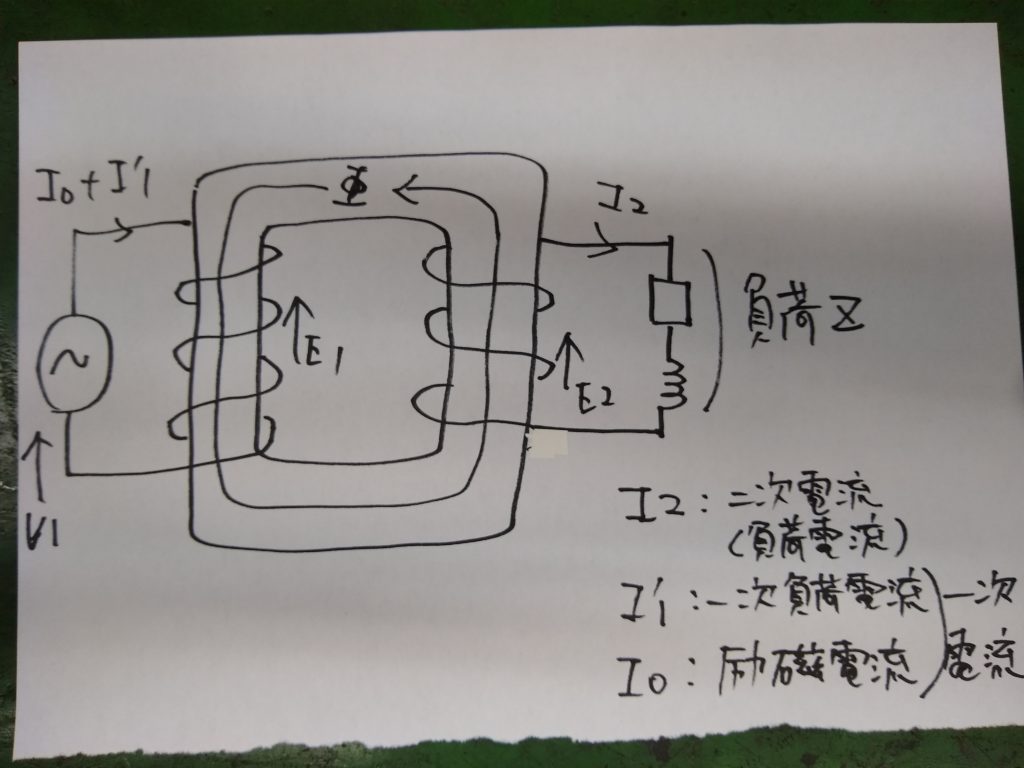
磁束Φが変化すると一次巻線の誘導起電力E1と、電源電圧V1のバランスが崩れます。これを補うため、磁束Φの変化を打ち消す新たな起磁力n1I’1が一次巻線に生じます。
このとき一次巻線に流れる電流I’1を「一次「負荷電流」といいます。
二次巻線に生じる起磁力n2I2とそれを打ち消すために一次巻線に生じる起磁力n1I’1とは等しく、次の関係が成り立ちます。
n2I2=n1I’1
一次巻線には、この一時負荷電流I’1と、励磁電流Ioが流れます。両者を合わせて「一次電流」といいます。
また、巻数比、変圧比、二次電流/一次負荷電流との間には次の関係が成り立ちます。

漏れリアクタンスと巻線抵抗
これまでの説明では、鉄心を通る磁束がすべて一次、二次巻線を貫くものと考えてきました。実際の変圧器では図のように鉄心から外に漏れる「漏れ磁束」を考慮する必要があります。
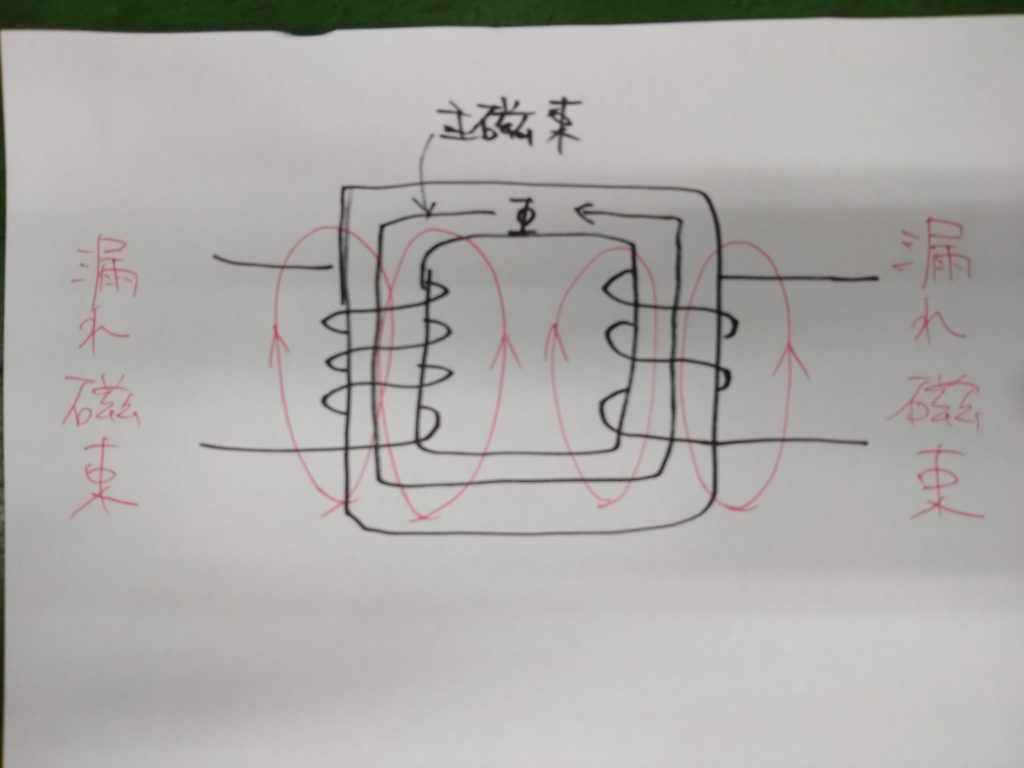
漏れ磁束は、それぞれの巻線でリアクタンスとして作用します。このリアクタンスを「漏れリアクタンス」といいます。
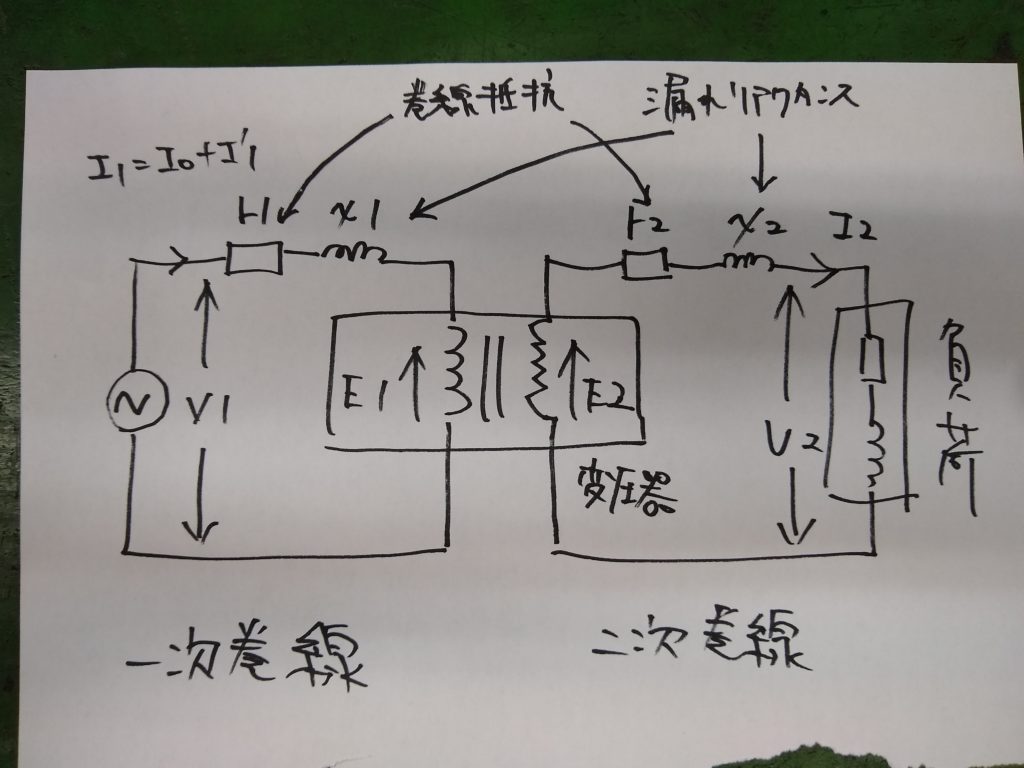
このほかに、巻線自体がもつ抵抗(巻線抵抗)も考慮すると、変圧器は次のような回路図で表されます。
励磁コンダクタンスと励磁サセプタンス
実際の変圧器では、漏れリアクタンスや巻線抵抗のほかにも、「鉄損」と呼ばれる電力損失を生じます。
この鉄損は、励磁電流Ioの通る並列回路を設けることで回路図に表すことができます。
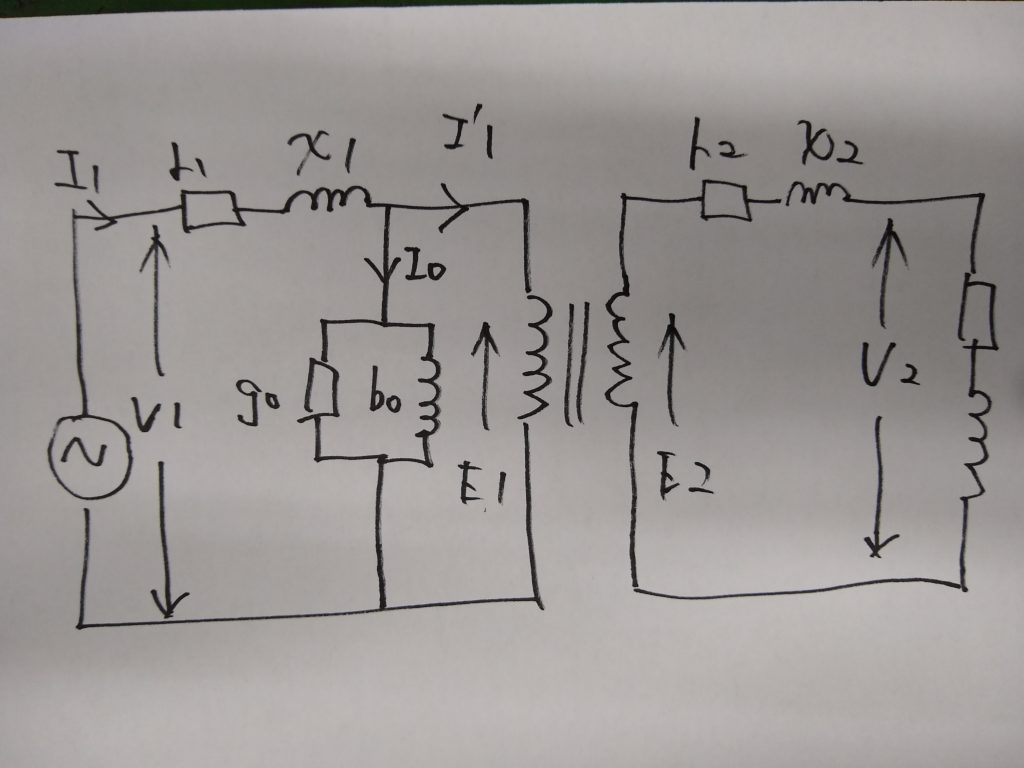
回路図のうちgoを「励磁コンダクタンス」boを「励磁サセプタンス」といいます。
goやboは値が大きいほどIoが大きくなる=電流の流れやすさを示す数値で、単位にはジーメンス(S)を用います。
また、両者の合成を「励磁アドミタンス」といいます。
変圧器の等価回路
変圧器の等価回路
下の回路図において、変圧器の巻数比をαとすれば、誘導起電力E1、E2の間と電流I’1、I2の間にはそれぞれ次の関係式が成り立ちます。
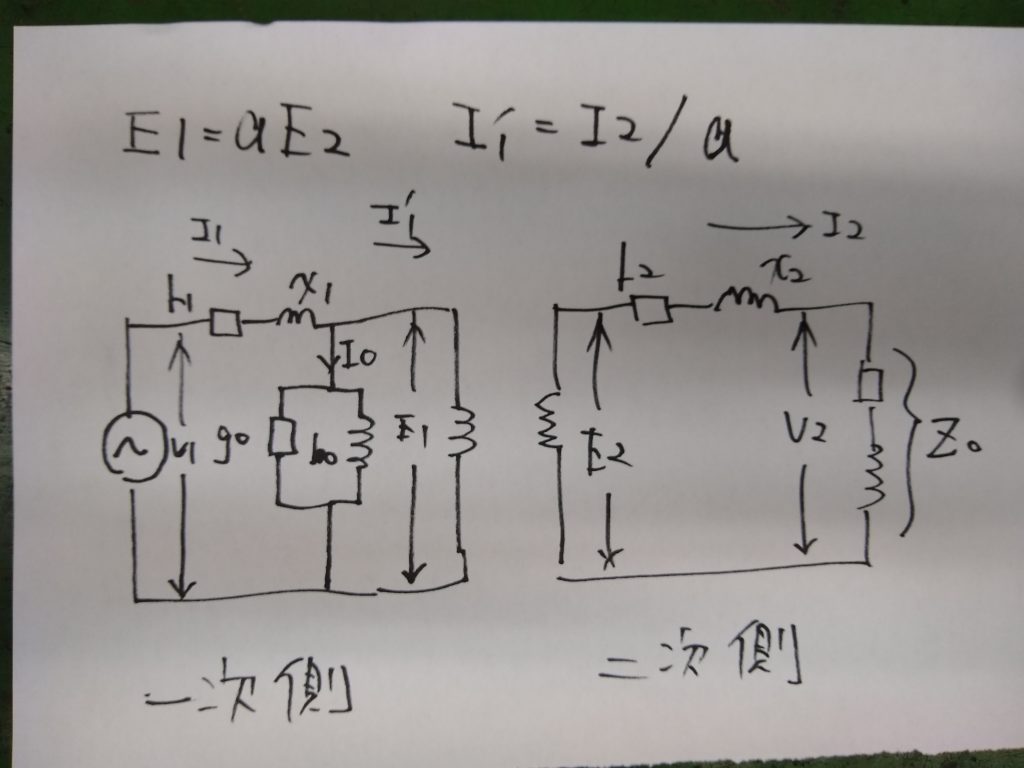
E2をα倍し、I2を1/α倍すれば、この回路図から変圧器を取り除き、一次側と二次側をくっつけることができるようになります。
そのためには、E1=αE2、I’1=I2/αが成り立つように二次側のインピーダンスと負荷電圧を適切な値に変換します。この変換を「二次を一次に換算する」といい、換算後の回路を「変圧器の等価回路」といいます。
二次を一次に換算(二次側の値を調整)
・負荷電圧V2をα倍する
・二次電流I2を1/α倍する
・r2、x2、Zoをα^2倍する
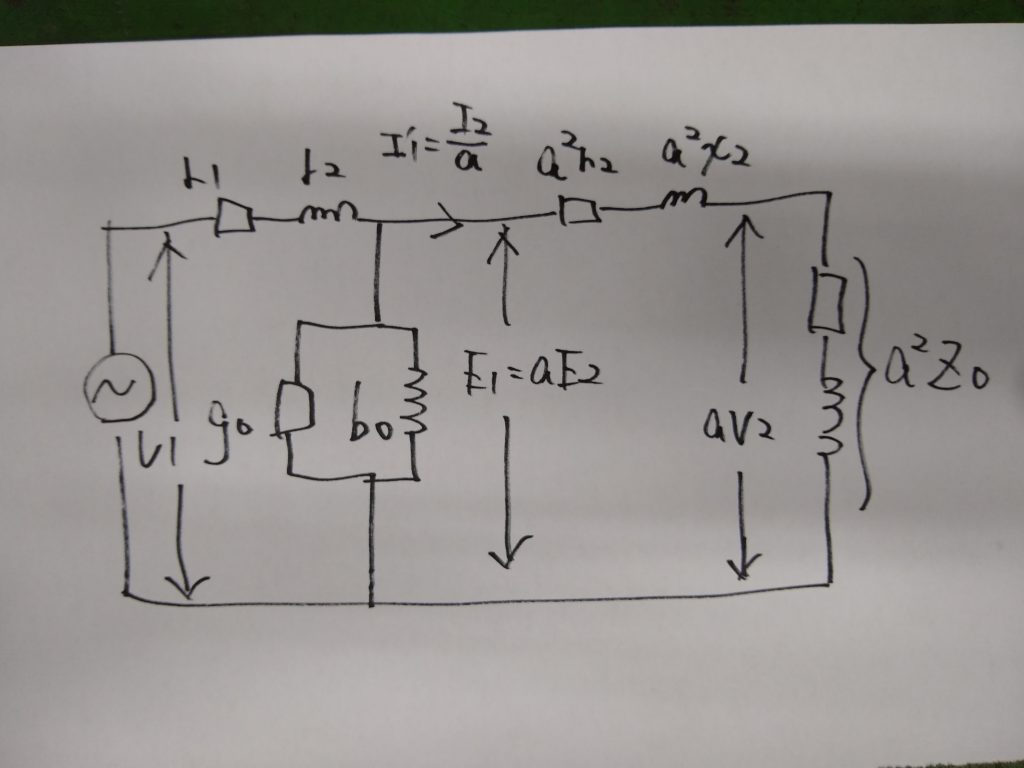
一次を二次に換算(一次側の値を調整)
・電源電圧V1を1/α倍する
・r1、x1、を1/α^2倍する
・go、bo、をα^2倍する
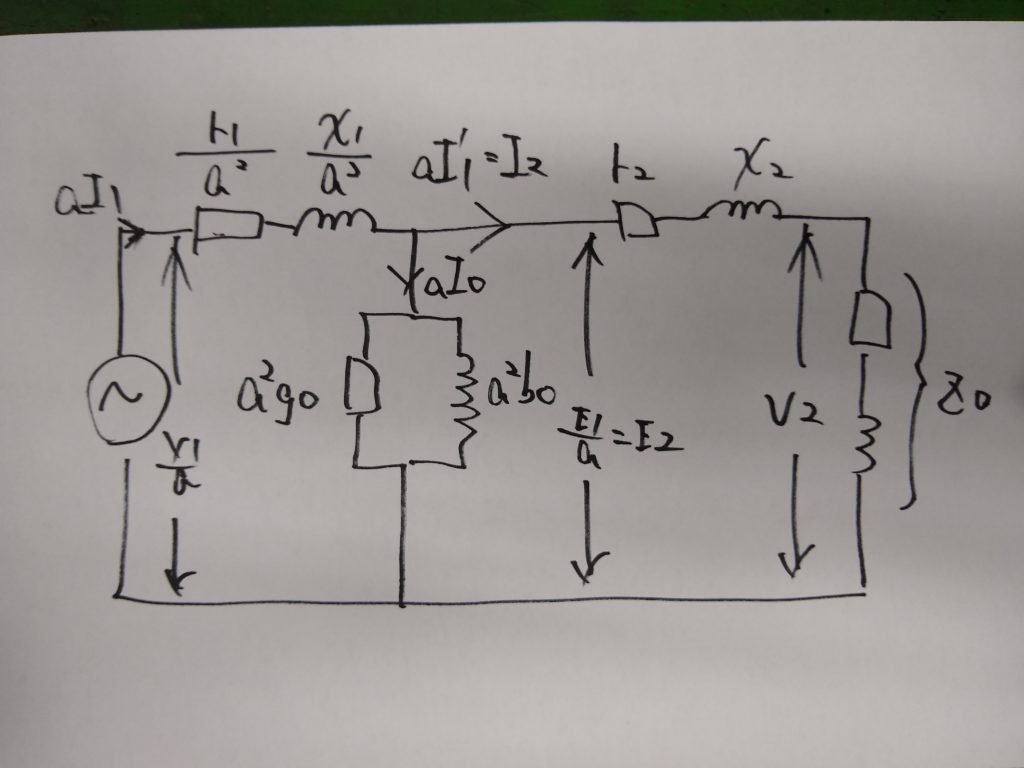
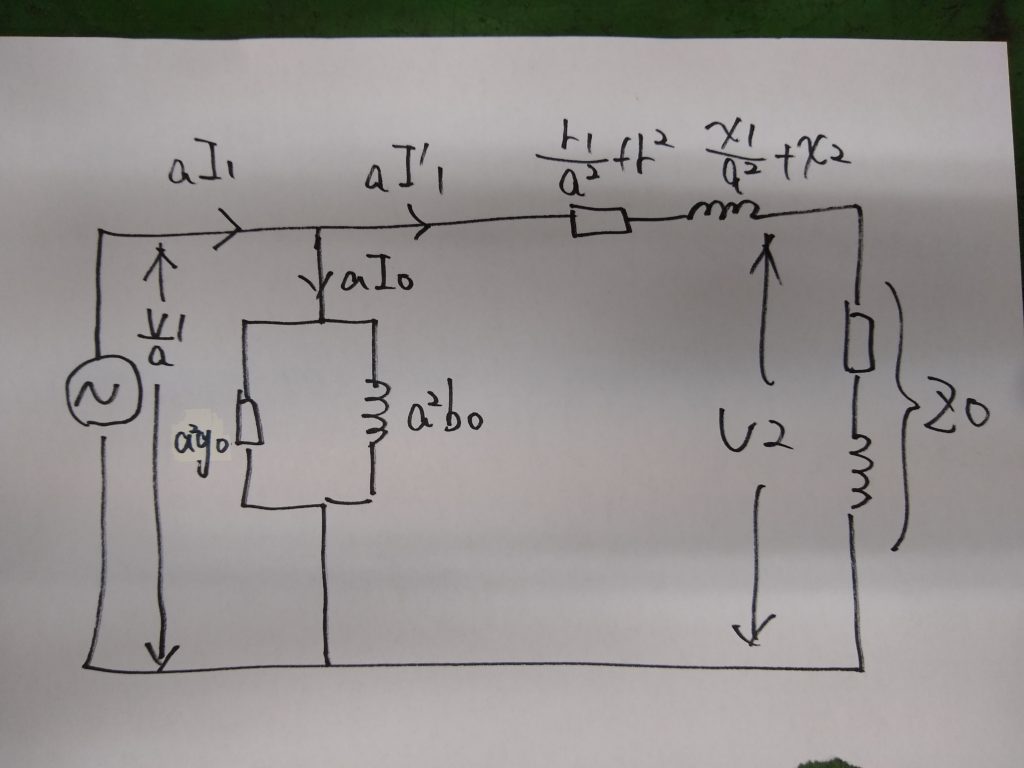
簡易等価回路
図のように励磁アドミタンスの並列回路を電源側に移動すると一次と二次の漏れリアクタンスと巻線抵抗をまとめて扱うことができ、計算が簡単になります。
このような回路を「簡易等価回路」といいます。
電圧変動率
電圧変動率とは
変圧器の二次側にあらわれる負荷電圧は一次電圧が同じ場合でも接続する負荷によって変化します。「電圧変動率」は、この変化の程度を示す値です。
電圧変動率を測定するにはまず変圧器の二次側に負荷を接続して指定された電流、力率、定格周波数のもとで負荷電流が定格値になるように一次端子電圧を加えます。
次に一次端子電圧は変えないで負荷を取り去り、二次電圧を測定します。このときの二次端子電圧をV20、また定格二次電圧をV2nとすれば、電圧変動率εは次の式で表されます。
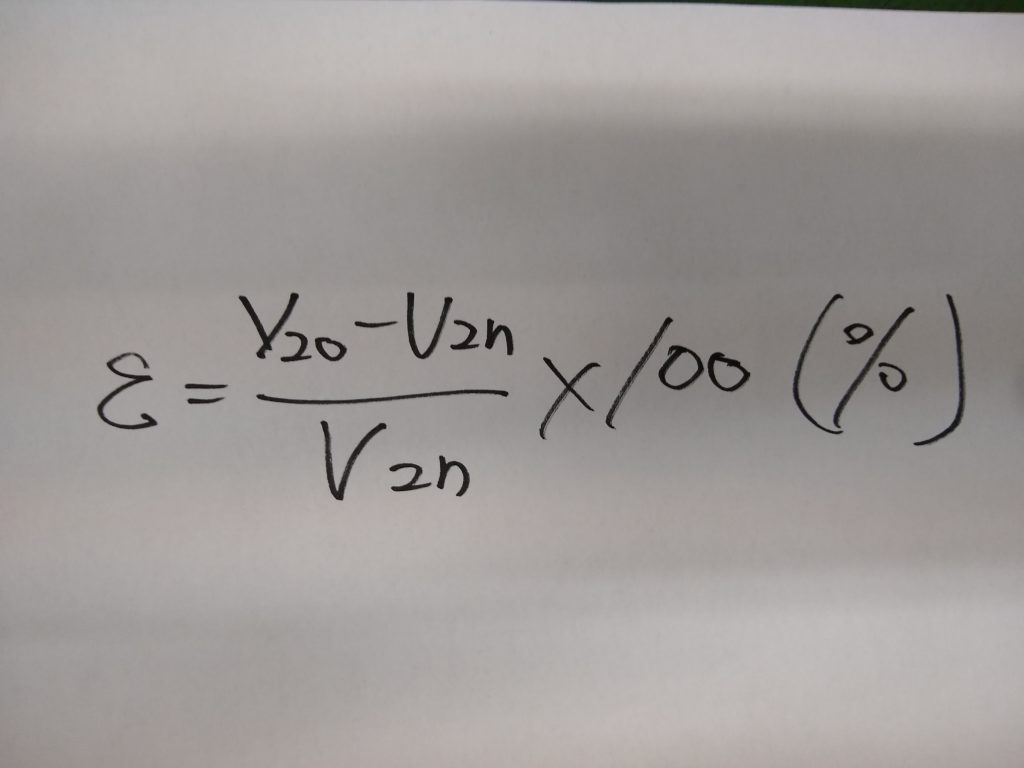
安定した電圧を負荷に供給するには変圧器の電圧変動率は小さい方が望ましいといえます。
インピーダンス降下と電圧変動率
負荷電圧が変動するのは、変圧器の巻数抵抗や漏れリアクタンスによって電圧降下が生じるためです。
そこで、次のような簡易等価回路を用いて、電圧降下をもとめてみましょう。
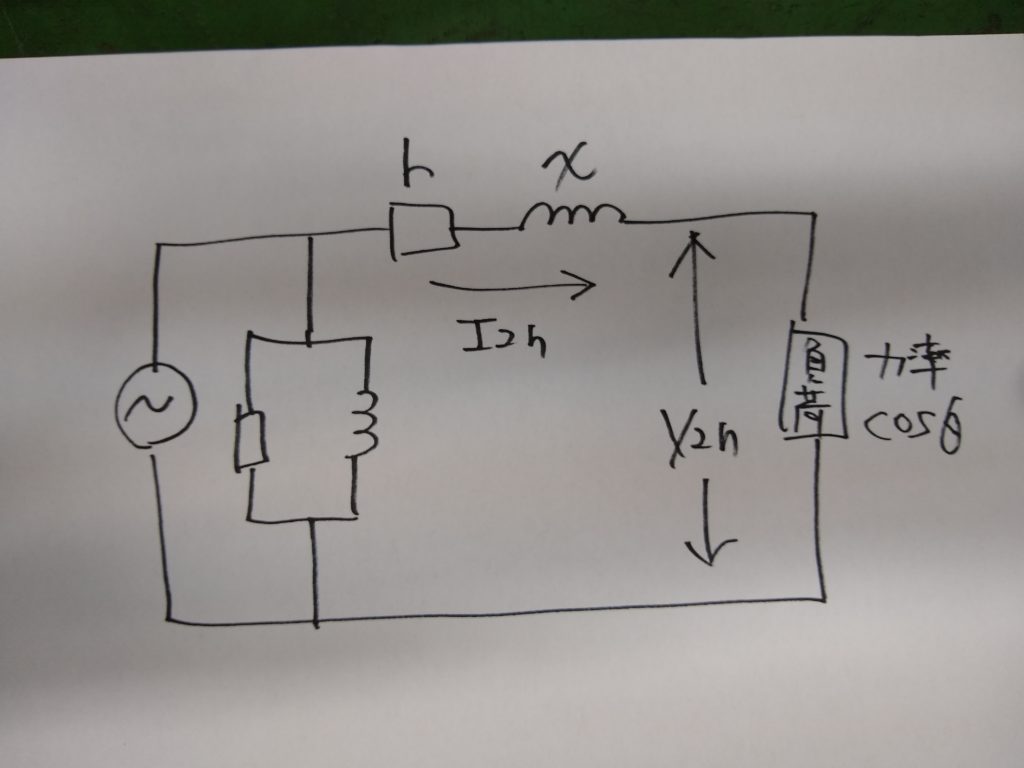
巻線抵抗rと漏れリアクタンスxによる電圧降下をそれぞれ「抵抗降下」「リアクタンス降下」といいます。
これらはそれぞれ次のように求めることができます。
抵抗降下 ⇒ rI2n(V)
リアクタンス降下 ⇒ xI2n(V)
ここで、二次電圧と二次電流、電圧降下の関係をベクトル図で表すと次のようになります。
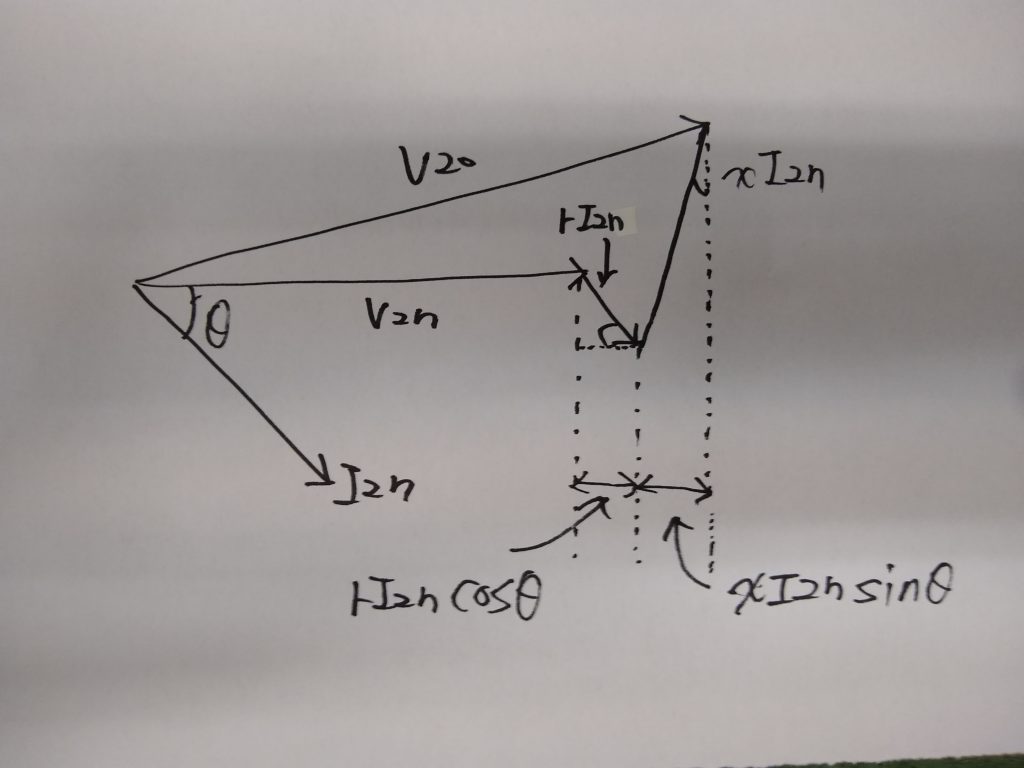
V2nとV20の位相差を無視すれば、電圧降下の合計は次のように求める事ができます。
rI2ncosθ+xI2nsinθ
したがって、電圧変動率は次のように求める事が出来ます。
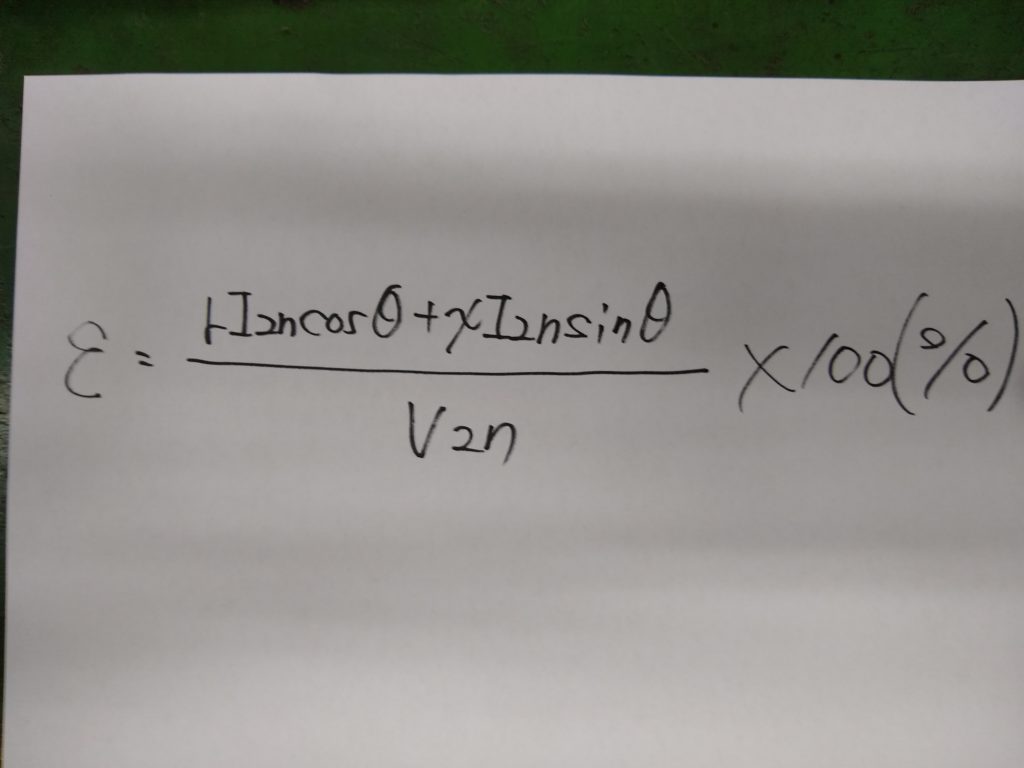
百分率インピーダンス降下と電圧変動率
抵抗降下やリアクタンス降下を定格二次電圧に対する比の百分率で表したものを、それぞれ「百分率抵抗降下」「百分率リアクタンス降下」といいます。

百分率抵抗降下と百分率リアクタンス降下を使うと、電圧変動率εは簡潔に表すことができます。
変圧比のインピーダンスは、短絡試験の測定結果から求めるため、短絡インピーダンスともいいます。
また、定格二次電圧に対する短絡インピーダンスによる電圧降下の比の百分率を「百分率短絡インピーダンス」といいます。
百分率抵抗降下pと百分率リアクタンス降下qは、それぞれ百分率短絡インピーダンス%Zの抵抗成分とリアクタンス成分で、以下の関係がなりたちます。
%Z=√p^2+q^2(%)
変圧器の損失と効率
変圧器の損失
変圧器の内部で発生する電力損失は、大きく「無負荷損」と「負荷損」に分類できます。
無負荷損
二次側が無負荷の状態で、一次電圧を加えたときの損失。「鉄損」がほとんどを占めます。
また、鉄損は「ヒステリシス損」と「渦電流損」の合計です。
ヒステリシス損:鉄心内の磁束が変化するとき、磁気分子相互に生じる摩擦による損失
渦電流損:磁束変化によって鉄心内に生じる起電力による損失
ヒステリシス損と渦電流損は、一次電圧の2乗に比例します。また、ヒステリシス損は一次電圧の周波数に反比例し、渦電流損失は鉄心の鋼板の厚さの2乗に比例します。
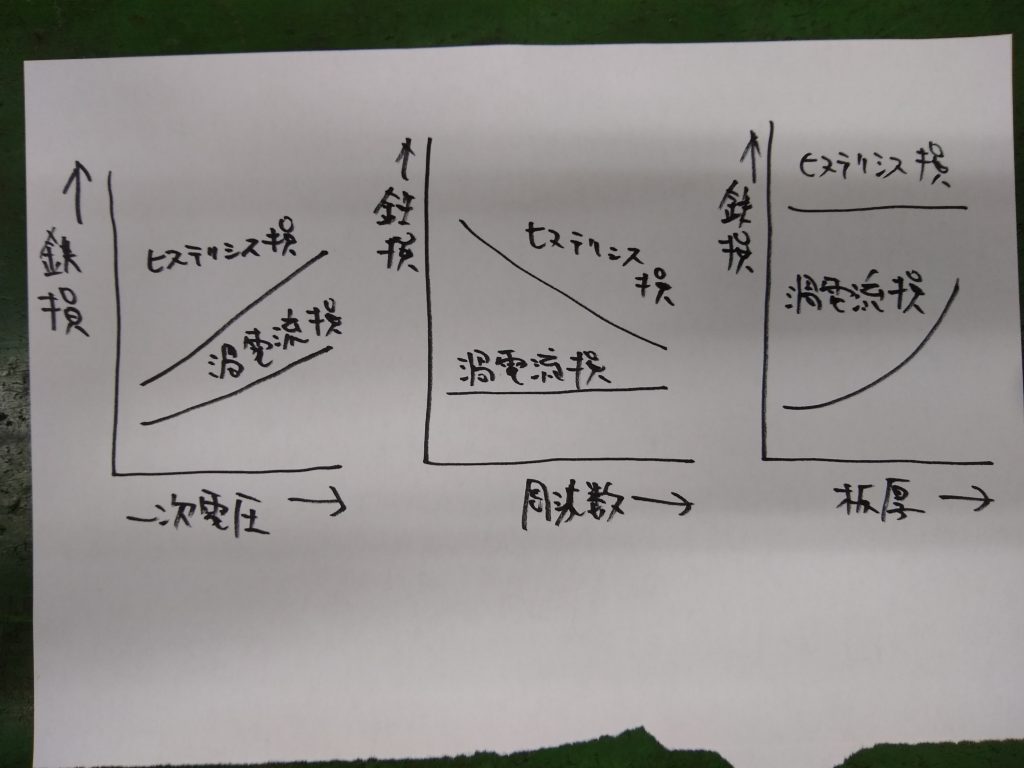
負荷損
二次側に負荷を接続したときに生じる損失。「銅損」がほとんどを占め、「漂遊負荷損」がわずかに加わります。
銅損:巻線抵抗によって生じるジュール熱
漂遊負荷損:漏れ磁束によって生じる損失
二次電流の大きさをI2、巻線抵抗の大きさをrとすれば、銅損の大きさはI2^2rで表されます。
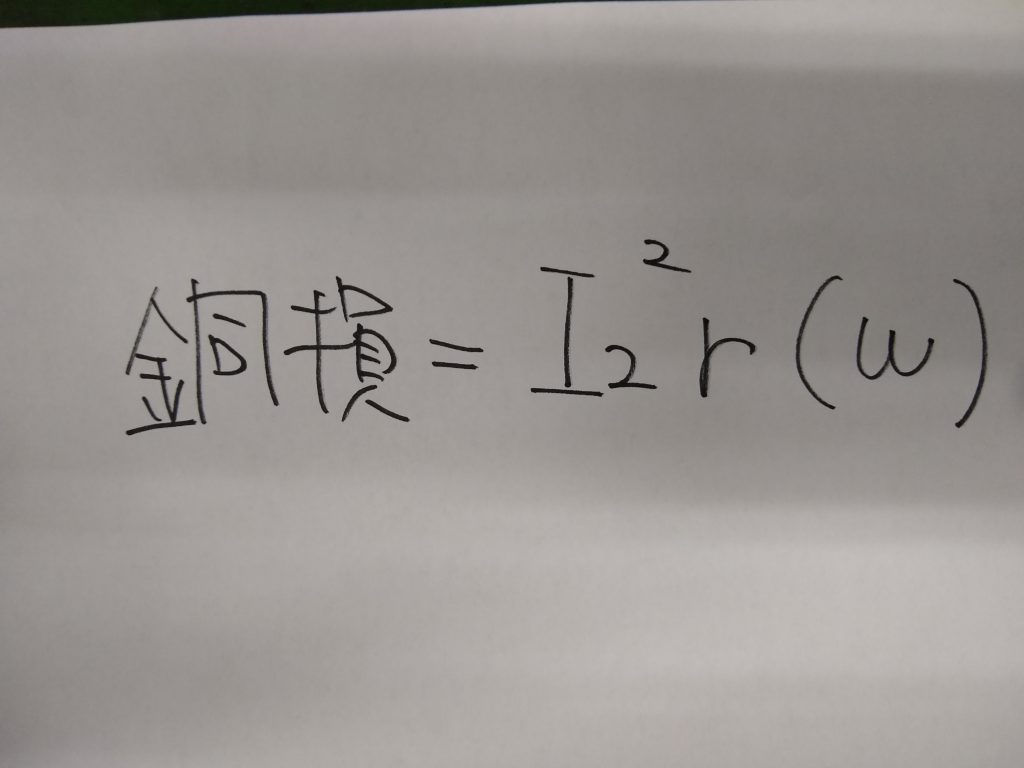
変圧器の効率
一次側の入力に対する二次側出力の比を変圧器の「効率」といいます。変圧器の効率は入力と出力が等しい時100%となります。
しかし実際には変圧器内部に損失があるため、出力は入力より少なくなります。
入力を出力と損失の和と考えれば、変圧器の効率は次式で表せます。

最大効率の計算
変圧器の効率が最大になるための条件を考えてみましょう。
二次電流をI2、二次で夏をV2、負荷力率をcosθ、無負荷損をpo、負荷損をp1として、変圧器の効率ηを次式で表します。

上の式より変圧器の効率は、Po/I2+I2rが最少のとき最大になります。
Po/I2+I2rが最少になるのは、
Po=I2^2r
のときです。したがって変圧器の効率は、無負荷損と負荷損が等しいとき最大となります。
変圧器の平行運転
変圧器の平行運転
2台以上の変圧器を並列に接続して運転する場合を平行運転といいます。
平行運転を行う各変圧器は、一般に次の条件にしたがって接続します。
・各変圧器の極性が一致する
・各変圧器の変圧比が等しい
・各変圧器のインピーダンス電圧(または百分率短絡インピーダンス)が等しい
・抵抗巻線と漏れリアクタンスの比が等しい
・三相結線では各変圧器の相回転と角変位が等しい
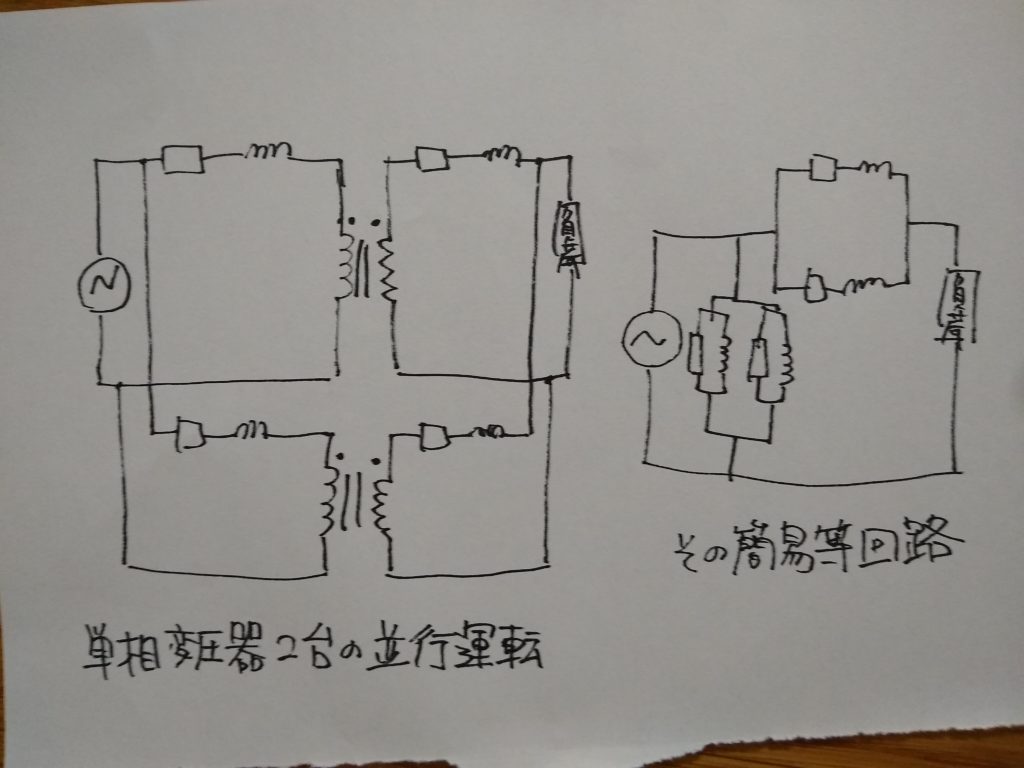
各変圧器の極性が一致している
変圧器の一次巻線に表れる誘導起電力が図のように同じ方向の場合を「減極性」といい、異なる場合を「加極性」といいます。
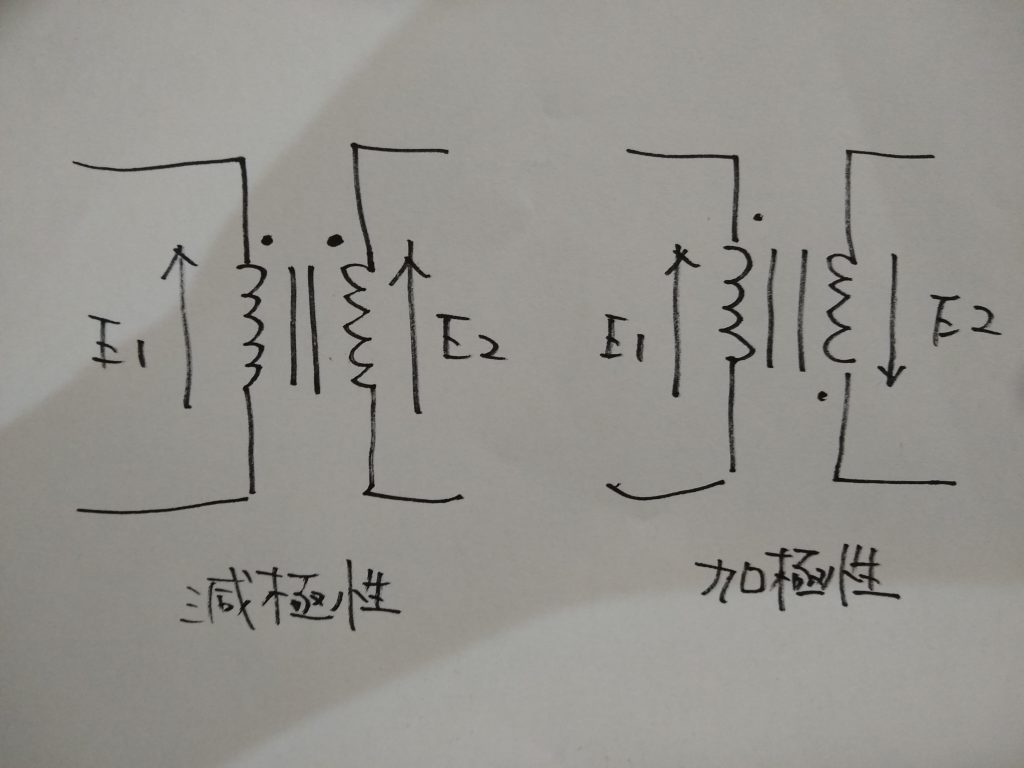
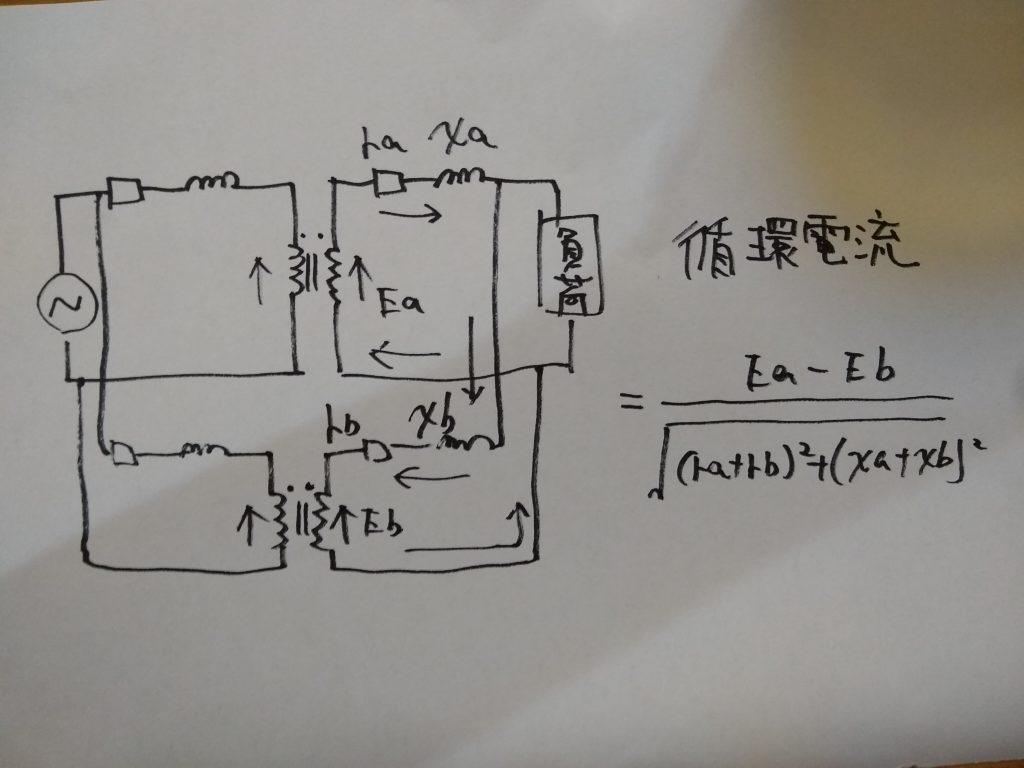
変圧器の一方の端子をもう一方の変圧器の異なる極性に接続してしまうと各変圧器の間に次のような循環電流が流れ、巻線の焼損などの原因となります。
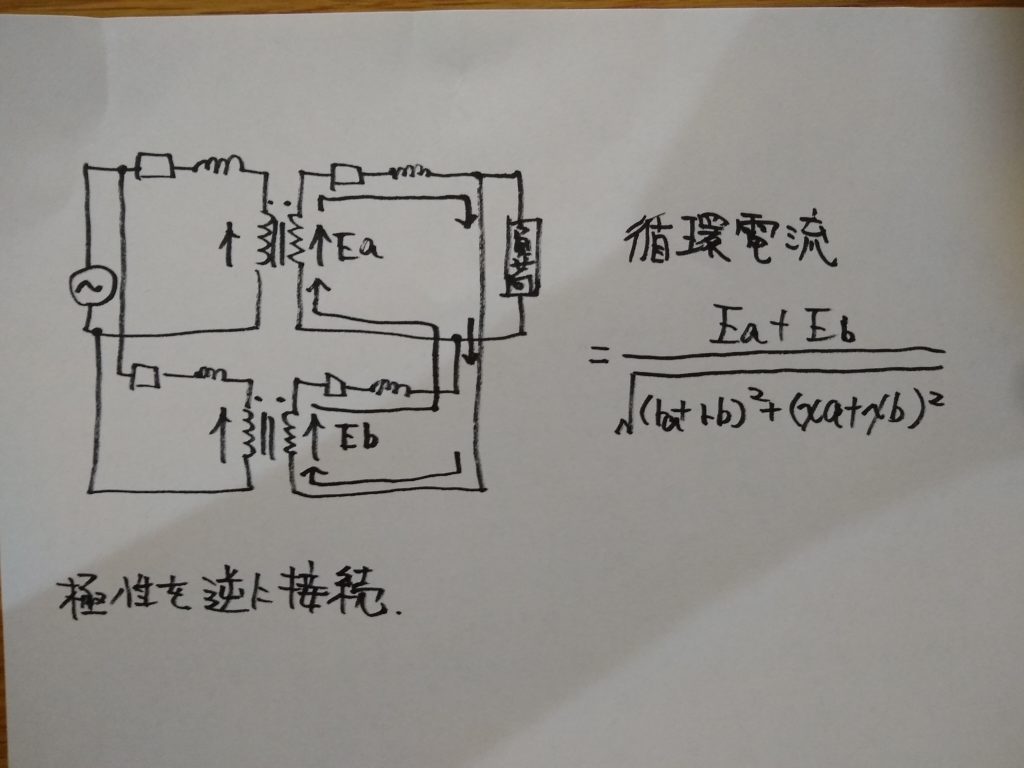
各変圧器の変圧比が等しい
変圧比が異なると二次側に異なる起電力が誘導されるため、その差から生じる循環電流が流れます。
各変圧器のインピーダンス電圧が等しい
平行運転では、各変圧器が定格容量(単位:VA)に比例した負荷電流を分担するとき、もっとも効率よく運転できます。
そのためには各変圧器のインピーダンス電圧(インピーダンス×定格負荷電流)が等しくなればよいのです。
なお、百分率インピーダンス降下(または百分率短絡インピーダンス)が等しければ、インピーダンス電圧も等しくなります。
巻線抵抗と漏れリアクタンスの比が等しい
抵抗とリアクタンスの比が異なると各変圧器が分担する電流に位相差が生じ、効率が悪くなります。
相回転と角変位が等しい(三相結線の場合)
この条件により以下の三相結線の組み合わせでは平行運転ができません。
・Δ-Y と Δ-Δ または Y-Δ と Δ-Δ
・Δ-Y と Y-Y または Y-Δ と Y-Y
・Δ-Y と V-V または Y-Δ と V-V
単巻変圧器
単巻変圧器のしくみ
図のように1本の連続した巻線を用いて、その一部を一次側と二次側が共有する変圧器を「単巻変圧器」といいます。

一次と二次の共通部分の巻線を「分路巻線」といい、共通しない部分を「直列巻線」といいます。
図のようにV1を一次側とすれば直列巻線には二次電流I2が流れ分路巻線には電流I1-I2が流れます。
分路巻線の巻数をnc、直列巻線の巻き数をnsとすれば、単巻変圧器の巻数比、変圧比は次のように表せます。
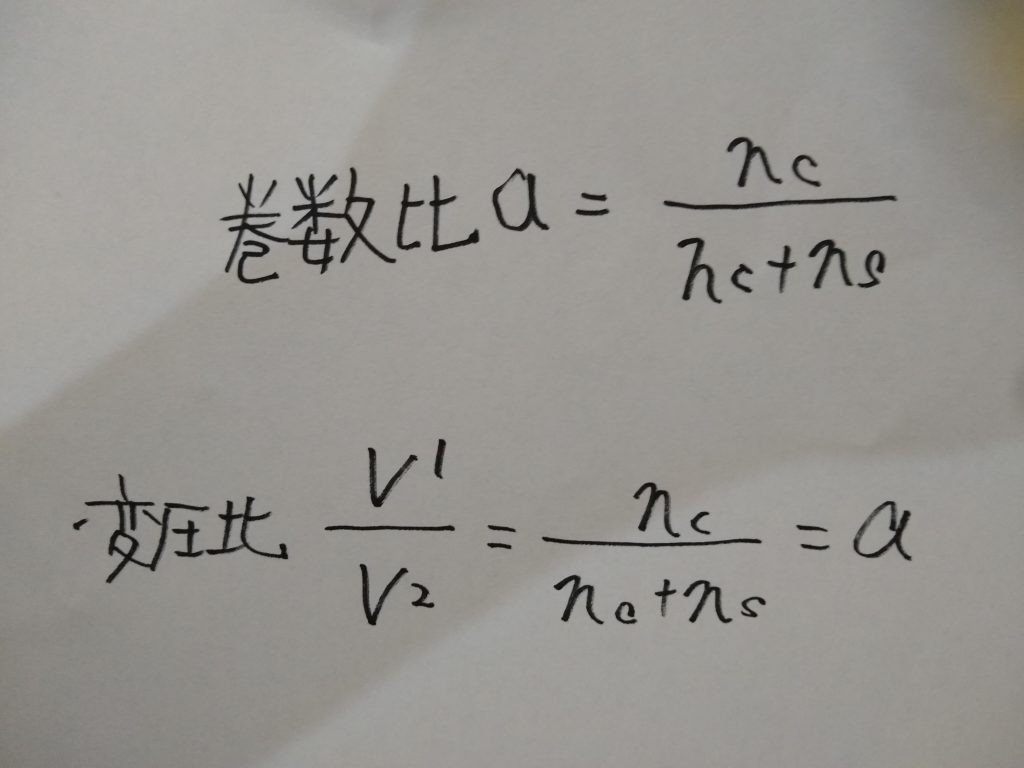
なお、一次電流I1は励磁電流Ioに一次負荷電流I’1を加えたものです。一次負荷電流の大きさI1と二次電流の大きさI2の比は次のようになります。
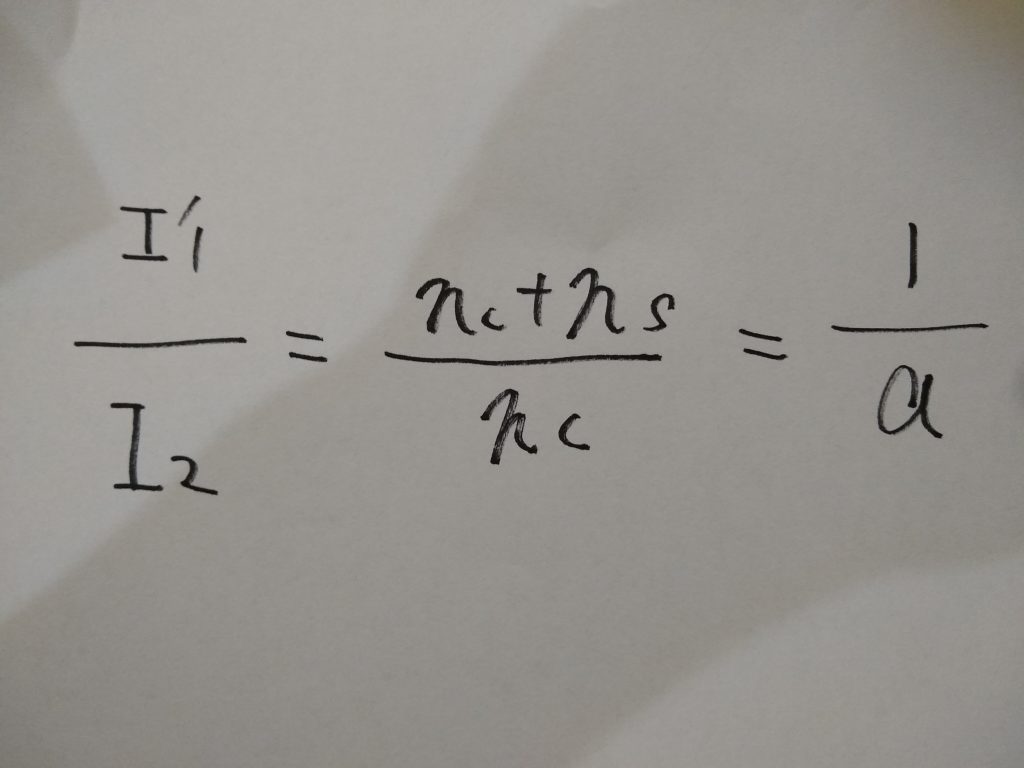
変圧器の三相結線
変圧器の三相結線
三相交流を変圧するには単相変圧器を3台一組にして三相に接続する方法と三相変圧器1台を用いる方法があります。
三相変圧器のほうが経済的なのでどちらかというと三相変圧器がよく用いられます。
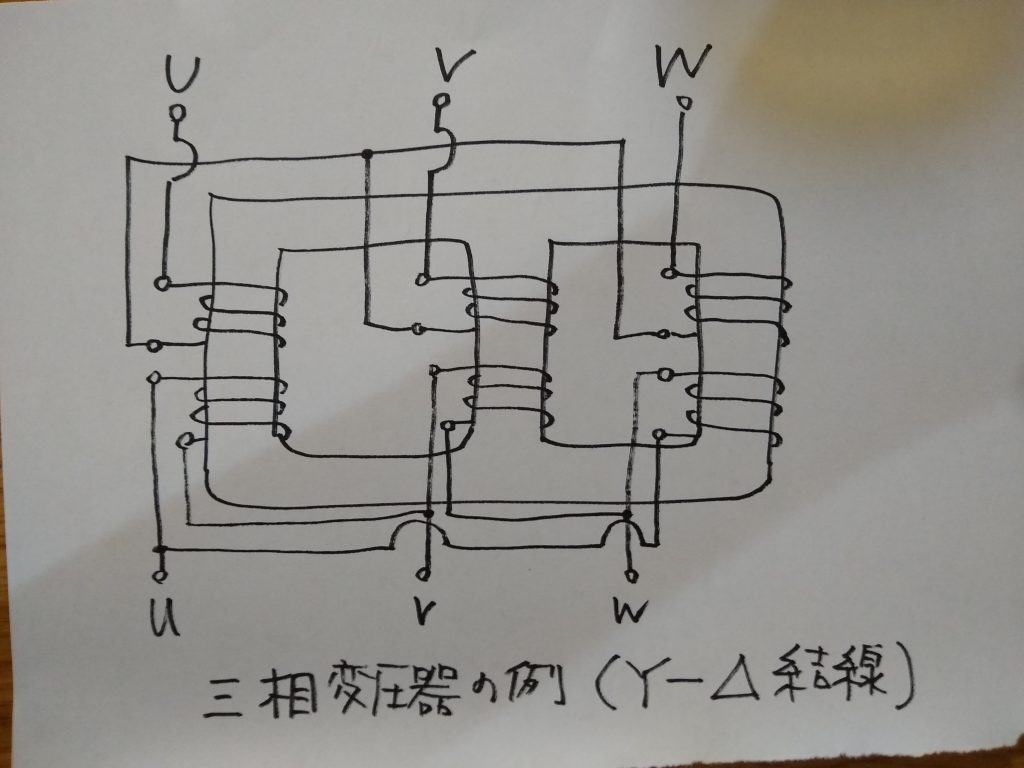
三相の結線方式にはY結線とΔ結線があります。一般にY結線は中性点を接地できるのが利点ですが、第3調波電流が流出してしまう欠点があります。
Δ結線はその逆で中性点接地が出来ない代わり、第3調波電流を外部に流しません。
このようにY結線とΔ結線には一長一短があるため、変圧器の用途に応じて使い分けられます。
また、一次側と二次側を異なる結線にする場合もあります。

これらのうち、Y-Y結線は通常は用いられず、代わりにY-Y-Δ結線がよく用いられています。
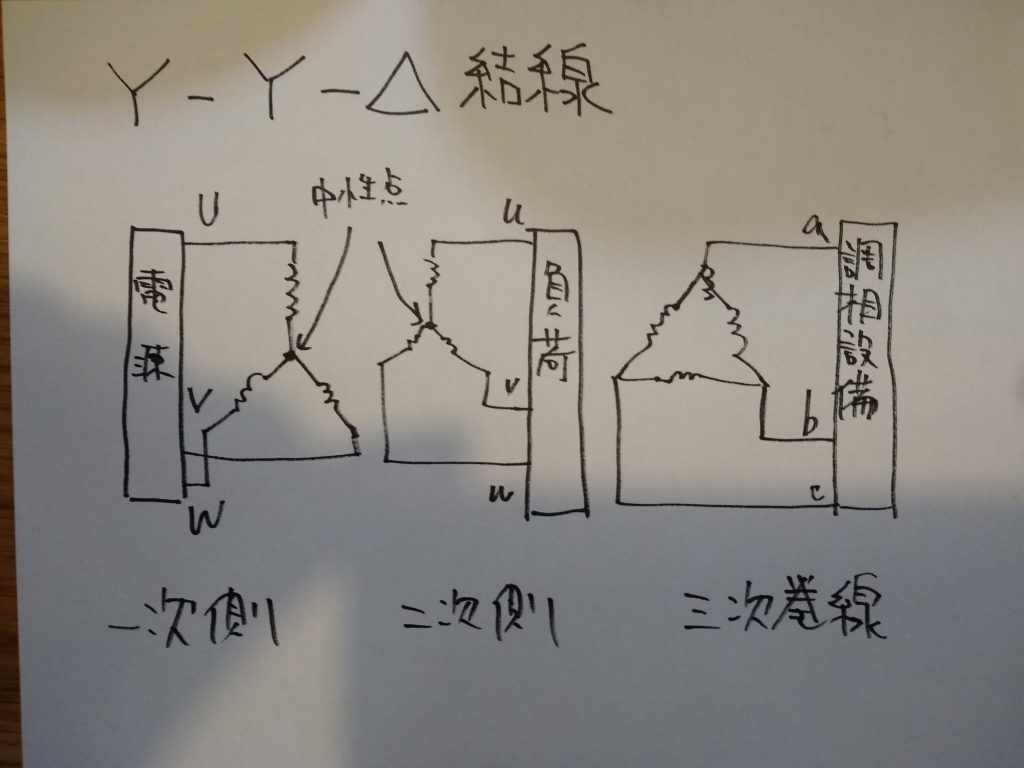
Y-Y-Δ結線は、Y-Y結線した変圧器にΔ結線にした三次巻線を追加したものです。
Y-Y結線
特徴:一次、二次ともに中性点を接地できる。第3調波の影響がある。
用途:通常は用いられない。
Y-Y-Δ結線
特徴:一次、二次ともに中性点を接地でき、三次結線で第3調波の影響も防止できる。
用途:変電所の主変圧器など。
Δ-Δ結線
特徴:第3調波による影響がない。中性点接地できないため高電圧には不向き。
用途;小容量の配電用変圧器など。
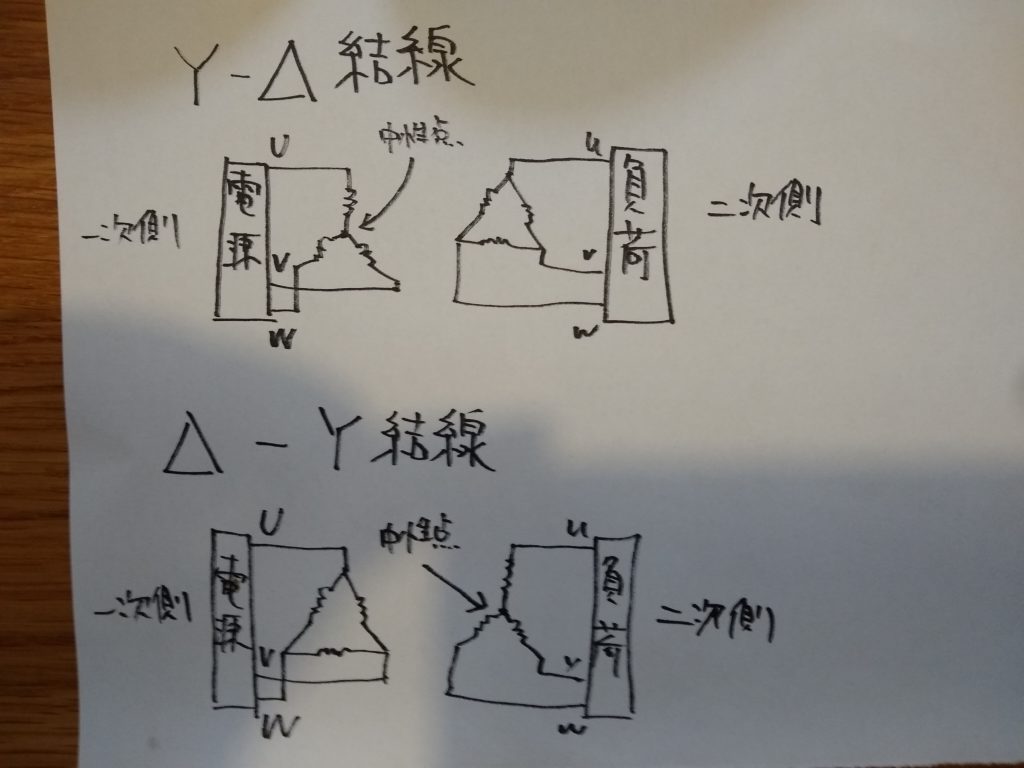
Y-Δ結線
特徴:一次側の中性点を接地できる。二次側がΔ結線になるので第3調波による影響がない。二次線間電圧は一次線間電圧より30°位相が遅れる。
用途:降圧用の変圧器など。
Δ-Y結線
特徴:二次側の中性点を接地できる。一次側がΔ結線になるので第3調波による影響がない。二次線間電圧は一次線間電圧より30°位相が進む。
用途:昇圧用の変圧器など。
V-V結線の利用
図のようにΔ-Δ結線から一相を除いたものをV-V結線といいます。
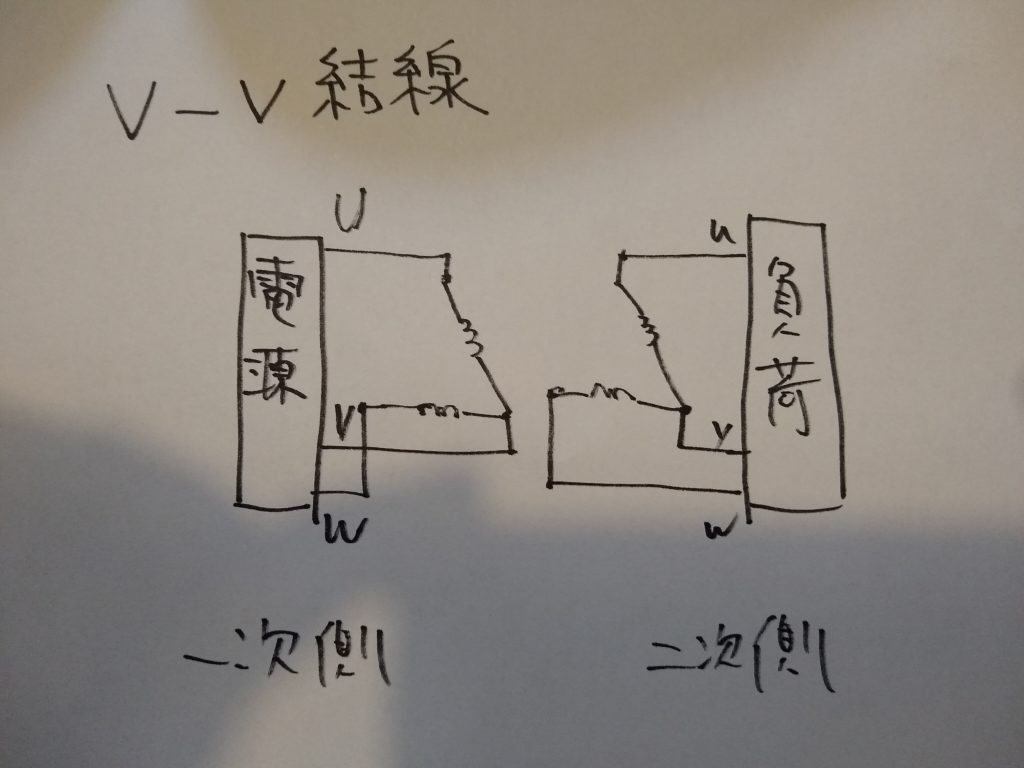
V-V結線は2台の単相変圧器で三相を変圧する場合に利用します。1台の単相変圧器の定格容量をP(VA)とすれば、単相変圧器3台一組をΔ-Δ結線したときの出力は、3P(VA)となります。
一方、単相変圧器2台一組をV-V結線した場合の出力は2P(VA)にはならず、√3P(VA)となります。これはΔ-Δ結線のときの約55%(√3/3)です。
また、本来2台分の容量=2P(VA)があるにもかかわらず√3P(VA)しか出力できないので、V-V結線のときの変圧器の利用率は、
√3P/2P=約0.866
のように低くなります。